teorema vieta

Teorema I. Wyeth pentru ecuația de gradul doi de mai sus.

Rădăcinile cantitate redusă ale ecuației pătratice x 2 + px + q = 0 este egal cu al doilea coeficient, luat cu semnul opus, iar produsul a rădăcinilor este egală cu termenul constant:

Găsiți rădăcinile ecuația de gradul doi de mai sus, folosind teorema lui Vieta.

EXEMPLUL 1) x 2 -x-30 = 0. Acest lucru a condus ecuație pătratice (x 2 + px + q = 0). al doilea coeficient p = -1. și q termen constant = -30. Mai întâi asigurați-vă că ecuația are rădăcini și rădăcinile (dacă există) vor fi exprimate în numere întregi. E suficient ca discriminante a fost un număr întreg pătrat perfect.

Găsim discriminant D = b 2 - 4ac = (- 1) 1 2 -4 ∙ ∙ (-30) = 1 + 120 = 121 = 11 2.

Acum, prin Teorema Vieta suma rădăcinilor ar trebui să fie egal cu al doilea coeficient, luat cu semnul opus, adică, (-p), iar produsul este egal cu termenul constant, adică (Q). apoi:

Exemplul 2) x 2 + 6x + 8 = 0. Ne-am dat ecuație pătratice cu un al doilea coeficient de p = 6 și q = membru gratuit 8. Asigurați-vă că există rădăcini intregi. Găsim D1 discriminant. ca al doilea coeficient - un număr par. D1 = -1 ∙ 2 8 = luna martie 9-8 = 1 = 1 2. discriminant D1 este un număr pătrat perfect 1. înseamnă rădăcinile ecuației sunt întregi. Reluăm rădăcinile teoremei Vieta: suma rădăcinilor este p = -6. și produs al rădăcinilor este egal cu q = 8. Acest număr -2 și -4.

Exemplul 3) x 2 + 2x-4 = 0. Aceasta a redus quadratic ecuație doilea coeficient p = 2. și q termenul constant = -4. Găsim D1 discriminant. ca al doilea coeficient - un număr par. D1 = 1 -1 ∙ luna februarie (-4) = 1 + 4 = 5. Discriminantul nu este un număr perfect, pătrat, astfel încât să putem concluziona. rădăcinile acestei ecuații nu sunt numere întregi și le găsesc imposibil teorema Vieta. Prin urmare, vom rezolva aceasta ecuatie, ca de obicei, prin formulele (în acest caz, formulele pentru cazul particular al chiar și al doilea factor). obținem:

Exemplul 4). Face o ecuație pătratică pentru rădăcinile, dacă x1 = -7, x2 = 4.

Exemplul 5.). Faceti o ecuație pătratică pentru rădăcinile sale, în cazul în care:

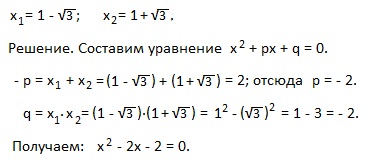
II. Teorema Wyeth pentru full ecuație pătratică ax 2 + bx + c = 0.

Rădăcinile sumă este egală cu minus b. împărțit de o. produs de rădăcini este egală cu. împărțit de o:

Exemplul 6). Găsiți suma rădăcinilor pătrate ale ecuației 2x 2 -7x-11 = 0.

Noi vedem că această ecuație va avea rădăcini. Este suficient pentru a face o expresie pentru discriminant, și fără să calculeze, doar pentru a se asigura că discriminant este mai mare de zero. D = 7 februarie -4 ∙ 2 ∙ (-11)> 0. Acum vom folosi teoremoyVieta pentru ecuații pătratice complete.

Exemplul 7). Găsiți produsul din rădăcinile unei ecuații pătratice 3x 2 + 8x-21 = 0.