Proprietățile funcției de analiza exemplul
Pentru a înțelege acest subiect, ia în considerare funcția. // se arată în graficul arată cum să funcționeze grafic pentru a determina proprietățile sale.
Proprietățile funcționale ale Parsează exemplului
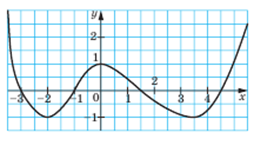
Domeniul Yavl a funcției. intervalul [3.5; 5,5].
Intervalul funcției valori yavl. intervalul [1; 3].
1. Când x = -3, x = - 1, x = 1,5, x = 4.5 valoarea funcției este zero.
Valoarea argument la care valoarea funcției este zero, numita funcție de zero.
//t.e. pentru aceasta simbolizarea -3, -1, 1,5; 4.5 sunt zero.
2. La intervale de [4,5; 3) și (1, 1,5) și (4,5; 5,5] grafic f este situat deasupra axei orizontale, și la intervale de (-3, -1) și (1,5; 4,5) sub axa abscisă, este explicat așa-la intervale [4,5; 3) și (1, 1,5) și (4,5; 5,5] functie are o valoare pozitivă, iar intervalele (-3, -1) și ( 1.5; 4.5) sunt negative.
Fiecare dintre aceste perioade (în cazul în care funcția ia valoarea aceluiași semn), menționată ca un decalaj de constantă funcției semn f.//t.e. de exemplu, dacă luăm intervalul (0, 3), atunci nu este un decalaj de semn constant al funcției.
În matematică, luate la intervale de funcția de căutare semn constant pentru a specifica un interval de lungime maximă. //T.e. timp (2, 3) este o perioadă a funcției semn constant f, dar ar trebui să fie incluse în intervalul de răspuns [4.5; 3) care cuprinde un spațiu (2; 3).
3. Dacă axa mobilă abscisei de la 4,5 la 2, se poate observa că graficul funcției se duce în jos, valorile adică ale funcției scade. // În matematică spunem că pe intervalul [4,5; 2] Funcția scade.
Odată cu creșterea x la 0 la 2 funcție grafic merge în sus, adică Valorile funcției crește. // În matematică spunem că pe intervalul [2; 0] Funcția crește.
Funcția f este în creștere pe un interval. Dacă o astfel încât x2> x1, satisface inegalitatea f (x2)> f (x1), pentru oricare două valori x1 și x2 argumentului acestui interval. // funcția de apel sau de creștere pe un interval. dacă, pentru orice valori argument ale acestui interval valoarea mai mare a argumentului corespunde unei valori mai mari a funcției ex .//. cu cât x, cu atât mai bine.
Funcția f este în scădere pe un interval. dacă, pentru oricare două valori x1 și x2 argumentului acestui interval astfel încât x2> x1, satisface inegalitatea f (x2) reducerea la un anumit interval de timp, în cazul în care, pentru orice valori argument ale acestui interval valoarea mai mare a argumentului corespunde valorii minime a funcției. //t.e. cu cât x, cu atât mai puțin.
În cazul în care funcția este în creștere în întreg domeniul de definiție, atunci aceasta se numește în creștere.
În cazul în care funcția este în scădere pe întregul domeniu, atunci aceasta se numește diminuare.
Exemplul 1. grafic respectiv crescătoare și descrescătoare funcții.
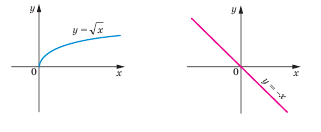
Determinarea yavl. dacă funcția liniară f (x) = 3x + 5 creștere sau în scădere?
Dovada. definiții Vosprolzuemsya. Să x1 și x2 sunt valori arbitrare ale argumentului și x1 Se obține prin substituirea f (x1) f (x2) = (x1 + 3 * 5) (3 * x2 + 5) = 3 * x1 + 3 5 5 * X2- = 3 * x2 = h1-3 * 1-3 * 3 * 7 = 3-21 = -19<0 Considerăm că f (x1) f (x2) <0,а значит f (x1) Am nevoie de ajutor la școală?