Legea atracției universale

1.10. Legea gravitației. mișcarea corpului sub acțiunea gravitației

Conform legii a doua a lui Newton cauza schimbări de mișcare, adică. E. Cauza accelerare a organelor, este o forță. Mecanicii sunt considerate forțe de diferite natură fizică. Multe fenomene și procese mecanice sunt determinate prin acțiunea gravitației.

Legea gravitației a fost descoperită de Newton în 1682. Înapoi în 1665, în vârstă de 23 de ani, Newton a sugerat că forțele care deține Luna în orbita sa, de aceeași natură ca și forțele care cauzează mărul cade la pământ. Conform ipotezei sale, între toate corpurile din univers, forțele de atracție (forța gravitațională), direcționată de-a lungul liniei care leagă centrele de masă (fig. 1.10.1). Conceptul centrului de greutate va fi definită strict în § 1.23. Corpul sub forma unei mase omogene a centrului minge coincide cu centrul bilei.

Forța gravitațională de atracție între corpuri.

În anii următori, Newton a încercat să găsească o explicație naturală pentru legile mișcării planetelor (a se vedea. §1.24), astronom publice J. Kepler din secolul al XVII-lea, și o expresie cantitativă pentru forțele gravitaționale. Știind cum se misca planetele, Newton a vrut să determine ce forțe acționează asupra lor. Această cale este numită problema inversă a mecanicii. Dacă obiectul principal al mecanicii este de a determina coordonatele corpului de masă cunoscută și viteza sa de la un anumit moment de forțele cunoscute care acționează asupra corpului și să specifice condițiile inițiale (problemă mecanică directă), în rezolvarea problemei inverse trebuie să determine care acționează asupra forțelor corpului, dacă este cunoscut cum se mișcă. Soluția acestei probleme a dus la descoperirea de legea lui Newton a gravitației universale.

Toate organismele atrag reciproc cu o forță direct proporțională cu masele lor și invers proporțională cu pătratul distanței dintre ele:

G = 6,67 · 10 -11 Nm 2 / kg 2 (SI).

Multe fenomene în natură sunt explicate prin influența forțelor de gravitație. Mișcarea planetelor din sistemul solar, sateliți artificiali, traiectoria rachetelor balistice, mișcarea corpurilor lângă suprafața Pământului - toate acestea pot fi explicate pe baza legii atracției universale și legile dinamicii.

Una dintre manifestările de forță atracției universale este forța de gravitație. Așa numitele corpuri de gravitație lângă suprafața Pământului. Dacă M - masa Pământului, R W - raza, m - masa corpului, forța gravitațională este egală cu

unde g - accelerația gravitațională la suprafața Pământului:

Forța gravitațională este îndreptată spre centrul Pământului. În lipsa altor forțe ale corpului cade liber pe Pământ cu o accelerație de cădere liberă. Valoarea medie a accelerației gravitației pentru diferite puncte ale suprafeței pământului este de 9,81 m / s 2. Cunoașterea accelerația gravitației, și Pământului raza (R H = 6,38 x 10 6 m) pentru calcularea masei pământului M.

Când distanța de la suprafața Pământului forța gravitațională a Pământului și accelerația gravitațională sunt schimbate invers proporțională cu pătratul distanța r spre centrul Pământului. Fig. 1.10.2 ilustrează variația forța gravitațională care acționează asupra unui astronaut într-o navă spațială cu distanța de la Pământ. Forța cu care astronaut este atras de pe pământ în apropierea suprafeței sale, este luată egală cu 700 N.

Schimbarea forța gravitațională care acționează asupra astronautul cu distanța de la Pământ

Un exemplu de un sistem de două corpuri care interacționează poate servi sistemul Pamant-Luna. Luna este de pe Pământ, la o distanță r A = 3,84 x 10 6 m. Această distanță este de aproximativ 60 de ori Z. raza R Pământului Prin urmare, o accelerație gravitațională cauzată de atracția pământului L., Luna orbita este

Cu o astfel de accelerare spre centrul Pământului, Luna se mișcă în orbita sa. Prin urmare, această accelerare este accelerația centripetă. Acesta poate fi calculat prin formula cinematic pentru accelerare centripete (vezi §1.6.):

unde T = 27,3 zile - perioada de revoluție a lunii în jurul pământului. Coincidența rezultatelor calculelor efectuate în diferite moduri, confirmă ipoteza de natură Newton forță uniformă care deține orbita Lunii, și gravitația.

câmpul gravitațional propriu al Lunii determină gravitațională accelerația g A pe suprafața sa. Masa lunii 81 de ori mai mică decât cea a Pământului, iar raza sa este de aproximativ 3,7 ori mai mică decât raza Pământului. Prin urmare, accelerația g h determinat prin expresia:

Într-o astfel de gravitate scăzută au fost astronauții care au aterizat pe Lună. Un om în astfel de condiții pot face salturi uriașe. De exemplu, în cazul în care o persoană de pe Pământ ricoșează la o înălțime de 1 m. Pe Lună, el ar putea sări până la o înălțime de 6 m.

Să considerăm acum problema sateliților artificiali pământ. sateliți artificiali se deplasează în afara atmosferei terestre, iar acestea sunt doar forța de gravitație de pe Pământ. În funcție de viteza traiectoria inițială a corpului exterior poate fi diferit. Considerăm aici doar cazul de mișcare a satelitului într-o orbită circulară în jurul Pământului. Astfel de sateliți zbura la altitudini de 200-300 km. și se poate presupune aproximativ distanța față de centrul pământului egală cu raza de R C accelerația centripetă Apoi prin satelit împărtășită prin forțe gravitaționale, este aproximativ egală cu accelerația cădere liberă g. Notăm viteza satelitului pe orbita Pământului prin υ1. Această viteză se numește prima viteză cosmică. Folosind formula cinematic pentru accelerația centripetă. obținem:

Conducerea la o astfel de viteză, satelitul se rotește în jurul pământului ar fi un moment

De fapt, perioada de rotație a satelitului într-o orbită circulară în apropierea suprafeței Pământului este ușor mai mare decât valoarea specificată, datorită diferențelor dintre raza efectivă a orbitei și raza Pământului.

Moțiunea satelitului poate fi privită ca o cădere liberă. astfel de proiectile de circulație sau a rachetelor balistice. Singura diferență este că viteza satelitului este atât de mare, încât raza de curbură a căii sale egală cu raza Pământului.

Pentru sateliții se deplasează pe trasee circulare, la o distanță considerabilă de pământ, gravitația scade invers proporțional cu pătratul razei r a traiectoriei. υ este viteza satelitului din starea

Astfel, în orbite înalte de viteza sateliților de circulație este mai mică decât orbita terestră joasă.

Perioada T a satelitului de referință este

Aici, T 1 - perioada de satelitul pe orbita joasa a Pamantului. satelit perioadă crește orbitale cu raza orbitei. Este ușor de calculat că orbita raza r, egală cu perioada orbitala circa 6,6 R Z. satelit va fi de 24 de ore. Satelitul cu o perioada orbitala de funcționare în planul ecuatorului, va atârna în continuare peste un moment dat, suprafața pământului. Astfel de sateliți sunt utilizate în sistemele de radio spațiu. Orbita rază r = 6,6 R H este numit geostaționară.

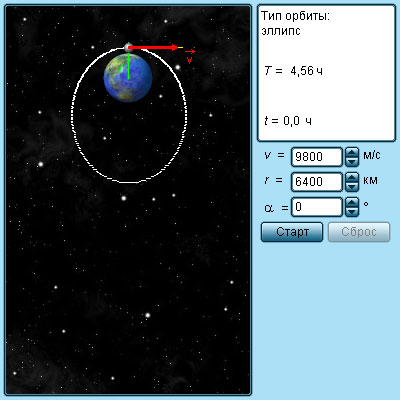
Modelul. mișcare prin satelit