definiția unui derivat
Acest articol va oferi concepte de bază, care se va baza în continuare pe toată teoria derivata unei funcții de o variabilă.
Path x - funcția argument f (x), și - un număr mic de non-zero.
(Citiți „Delta X“) se numește incrementarea argumentului. În figura linia roșie arată schimbarea în argumentul valorii lui x la valoarea (aici sunt vizibile numele argumentului „creștere“).
La trecerea de la valoarea argumentului la valoarea funcției, respectiv, variază de la subiect la monotonie segmentului. Diferența se numește o funcție increment f (x). care corespunde acestei creșteri a argumentului. Figura prezintă linia albastră funcția de creștere.
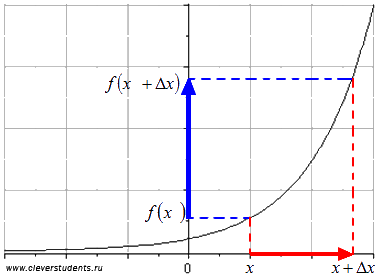
Luați în considerare aceste concepte într-un exemplu concret.
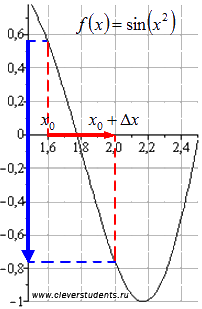
Să luăm, de exemplu, funcția. Fix un punct și incrementarea argumentului. În acest caz, incrementul funcției în tranziția de la încă să fie
Descreșteri a spus funcției de degradare pe intervalul.
Determinarea derivata unei funcții într-un punct.
Să presupunem că funcția f (x) definită pe intervalul (a, b). și - punctul acestei perioade. Derivata funcției f (x) într-un punct numit limita raportului dintre incrementului argumentul funcției cu increment. Indicat.
Când a fost ultima limită are o valoare finită specifică, atunci vorbim despre existența unui derivat de la un punct finit. Dacă limita este infinit, atunci spunem că derivatul este infinit în acest moment. În cazul în care limita nu există, atunci derivata funcției în acest moment nu există.
f funcție (x) se numește diferențiabilă în punctul în care acesta are un derivat finit în acesta.
Dacă funcția f (x) este diferențiabilă în fiecare punct al intervalului (a, b). funcția se numește derivabile pe acest interval. Astfel, orice punct x în intervalul (a, b) poate fi asociată cu valoarea funcției derivat de la acest punct, adică, suntem capabili de a defini o nouă funcție, care se numește derivata funcției f (x) pe intervalul (a, b).
Operația găsirii derivatului se numește diferențiere.
Egal distincție în natura conceptelor funcției derivat de la un punct și pe un interval: derivata funcției în punctul - acesta este numărul și derivata funcției în intervalul - este o funcție.
Găsiți derivata unei funcții într-un punct, folosind definiția.
Din moment ce sunt în căutarea unui derivat al funcției în intervalul, atunci răspunsul ar trebui să rândul său, funcția. Ia, în cazul în care x - orice număr din intervalul. Prin definiție, derivatul este o limită pentru raportul funcției increment a creșterii argumentului, pentru incrementarea argumentul tinde la zero:
Astfel, am ajuns la incertitudine. Pentru a găsi aceste limite folosind multiplicarea prin expresia conjugată urmată de aplicarea formulelor Acronimul multiplicarea acționării acestor termeni și abrevieri:
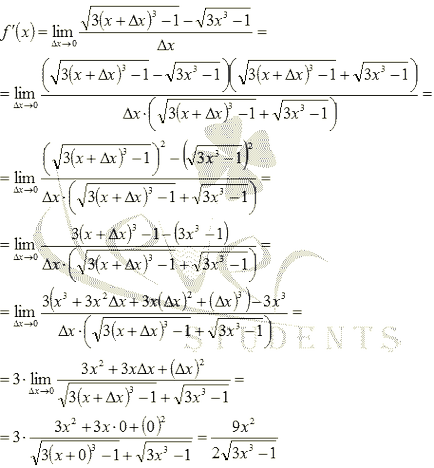
Să se concentreze pe un punct foarte important: domeniul funcției f (x) nu coincide întotdeauna cu domeniul derivatului. De notat că, în exemplul anterior, domeniul funcției este intervalul inițial și derivatul determinat în intervalul. Ceea ce vrem să spunem. Astfel încât atunci când diferențiind răspunsul ideal este: funcția este un derivat al funcției f (x) în intervalul
Pe baza definiției derivatului cu formula obținut mai multe tabele derivate funcții elementare de bază, care sunt foarte accelerează diferențierea. Conceptul de derivat este, de asemenea, utilizat în dovada regulilor de derivare.