Calculul triplu integrale

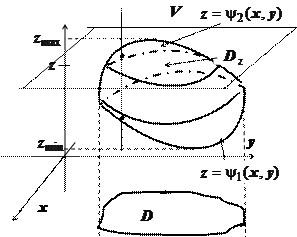
Să ne numim o regiune mărginită închis $ \ mathbf> \ textbf $, în cazul în care sunt îndeplinite două condiții. proiecție de $ \ mathbf> $ la orice coordonate plan, de exemplu, pe plan $ \ mathbf> $ - simplu domeniu de $ \ mathbf> $, precum și orice linie dreaptă perpendicular pe acest plan și care trece prin punctul interior de $ \ mathbf> $, cruci $ limita \ mathbf> $ în două puncte. Această regiune poate fi descrisă după cum urmează: $ V = \ stânga (\ dreapta) $ suprafață $ z = \ psi _1 (x, y) $ definită printr-o multitudine de puncte inferioare de intersecție a unei linii paralele cu axa de $ \ mathbf> $, limita de $ \ mathbf > $; suprafață $ z = \ psi _2 (x, y) $ - o multitudine de puncte de intersecție superioare).

$ \ Textbf $ această teoremă poate fi, așa cum am demonstrat teorema despre trecerea de la dublu parte integrantă a re: a stabili că, pentru integrantă reiterate pe formulele din partea dreaptă dețin toate proprietățile integralei, diviza regiunea de $ \ mathbf> $ pe un subdomeniu $ \ mathbf> _ (\ mathbf> = 1,2 ,, \ mathbf>) $, folosesc proprietățile aditiv și valoarea teorema medie, retrimiteți integral ca o sumă integrală pentru triplu $ \ stânga (^ n> \ dreapta) $ și du-te la limita ca $ d = \ mathop \ limits_ diam (V_i) \ la 0 $.

Dacă vopsea dublu integralei pentru simplul $ teren \ mathbf> \ quad \ stânga (a \ leqslant x \ leqslant b, \\ \ varphi _1 (x) \ leqslant y \ leqslant \ varphi _2 (x) \\ \ end> ​​\ dreapta .> \ right]> \ dreapta) $ sub forma de re-obține formula chiar mai detaliată pentru calculul triplu integral: $ \ iiint \ limits_V = \ iint \ limits_D ^> = \ int \ limits_a ^ b ^^ >> $.

Puteți, de asemenea, dovedi că triplă integrala poate fi reprezentat sub forma de re-integrare cu celelalte proceduri. Notăm $ z_ = \ mathop \ limits_, \; z_ = \ mathop \ limits_ $ adică valorile minime și maxime ale ordonatele punctelor pentru zona $ \ mathbf>) $, $ D_z $ - regiune plat obținută prin tăierea $ \ mathbf> $ avionul $ \ mathbf> $ = const. Apoi $ \ iiint \ limits_V = \ int \ limite _> ^ >> dxdy $. Desigur, pentru o anumită sarcină poate fi de preferat pentru a proiecta un $ \ mathbf> $ nu este pe planul $ \ mathbf> $, dar pe de altă parte de coordonate plan.

Exemple de rezolvare a problemelor

Calculăm aceeași integralei pentru alte formule pentru trecerea la o reiterate integrală: $ I = \ int \ limits_0 ^ h> = \ int \ limits_0 ^ h> = \ int \ limits_0 ^ h> = \ int \ limits_0 ^ h = $ intern dublu integrală - integralei funcției egal cu 1, astfel încât să fie egală cu suprafața cercului, rezultat prin tăierea conului plan $ z = $ const, ecuația delimitând cerc, zona $ s (D_z) = \ frac) = \ int \ limits_0 ^ h dz> = \ frac \ cdot \ left> \ dreapta |. _0 ^ h = \ frac $.

Această decizie sa dovedit a fi mai ușor; Am jucat pe faptul că integrandul nu depinde de $ \ mathbf> $ și $ \ mathbf> $.

A se vedea, de asemenea:

definiția invariant de divergență

Exemple de utilizare a coordonatelor cilindrice și sferice

Definiția unei integrale dublu

Și de suprafață cu două fețe. orientarea suprafeței

Du-te la conținut $ \ rightarrow \ rightarrow \ rightarrow $