WolframAlpha în triplă integrală rusă în wolframul, alfa

Pentru a găsi integralei triplu în Wolfram | Alpha, folosiți următoarea sintaxă (mai degrabă decât să integreze permis versiunea abreviată int):

• integra xyz DXDYDZ

Vă rugăm să rețineți că aici, precum și pentru integralelor duble. pentru Wolfram | Alpha este foarte importantă ordinea diferențelor de înregistrare dx, dy și dz în vyrazhnenii integrandul, care determină secvența de re-integrare.

În general, un rezultat care afișează Wolfram | Alpha, depinde de secvența în care se efectuează re-integrare (ordinea în care în scris dx, dy și dz). Comparați, de exemplu, exemplul anterior cu următorul text:

• integra dydzdx xyz

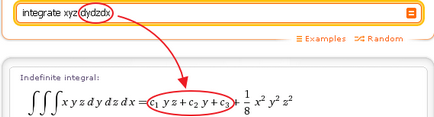
Pentru a calcula integrala tripla bine definit. trebuie să specificați în mod corespunzător limitele de integrare.

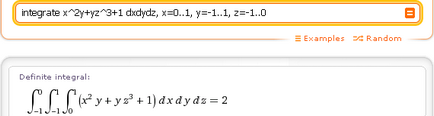
Dacă toate limitele constante de integrare. înregistrarea comandă dx, dy și dz nu contează. De exemplu,

• integra x ^ 2y + yz ^ 3 + 1 DXDYDZ, x = 0..1, y = -1..1, z = -1..0

Același lucru este valabil atunci când este vorba despre calculul integralelor triple, cu limite infinite:

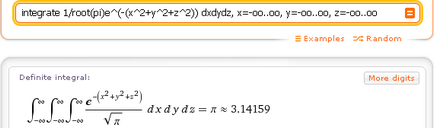
• integra 1 / rădăcină (pi) e ^ (- (x ^ 2 + y ^ 2 + z ^ 2)) DXDYDZ, x = -oo..oo, y = -oo..oo, z = -oo..oo

Cu toate acestea, în cazul dat în limitele variabile integrale triple de integrare. înregistrarea comandă dx, dy și dz devine din nou importantă. Nu trebuie să uităm că dx, dy și dz în calculul triplu integrale din Wolfram | Alpha trebuie neapărat să scrie în ordine inversă ordinii, care trebuie să fie re-integrarea în calculul triplu integrale. Și anume, așa cum se arată în acest exemplu:

• integra xy ^ 2 + yz ^ 2 + zx ^ 2 dzdydx, z = xy..root (x ^ 2 + 2y ^ 2), y = x ^ 2..root (x), x = 0..1

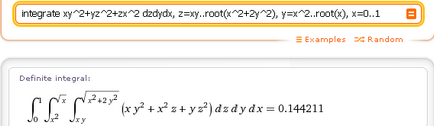
După cum puteți vedea, aici ordinea de calcul a triplu integrale, după cum urmează: în primul rând „ia“ integralei interioară a dz (limitele de integrare în care depind de x și y), apoi - prin dy (limite de integrare pentru variabila y depinde de x), și în cele din urmă " luate „în afara integralei peste dx. Acesta este motivul pentru care, la sfârșitul integrandul este o expresie dzdydx (secvența este importantă!).