triunghi dreptunghic
Picioarele unui triunghi dreptunghic: \ (a \), \ (b \)
Ipotenuza unui triunghi dreptunghic: \ (c \)
unghiuri ascuțite: \ (\ alpha \), \ (\ beta \)
unghi drept: \ (C \)
Zona unui triunghi dreptunghic: \ (S \)
Înălțime, a redus ipotenuzei: \ (h \)
Median: \ (\) \ (\) \ (\)
Raza cercului circumscris: \ (R \)
Raza cercului inscris: \ (r \)
triunghi dreptunghic este numit un triunghi în care un unghi al liniei drepte (egal cu \ (90 ^ \ Circ \)).
Părțile laterale ale triunghiului, formând un unghi drept se numesc picioare. iar partea opusă unghiului drept - ipotenuzei. În această figură, partea \ (AC \) și \ (BC \) sunt picioare, lateral \ (AB \) - ipotenuzei. Lungimile picioarelor sunt egale \ (a \) \ (b \). Lungimea ipotenuzei \ (c \).
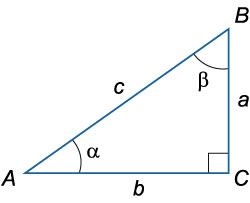
Cantitatea de unghiuri ascuțite ale unui triunghi dreptunghic este egal cu \ (90 ^ \ Circ \):
\ (\ Alpha + \ beta = 90 ^ \ Circ \)
Sinus unghi ascuțit într-un triunghi dreptunghic egal cu raportul dintre piciorul opus ipotenuzei:
\ (\ Sin \ alpha = \ mare \ frac \ normalsize \) \ (\ păcatul \ beta = \ mare \ frac \ normalsize \)
Cosinusul unghiului ascuțit într-un triunghi dreptunghic este egal cu raportul dintre ipotenuzei cu piciorul adiacent:
\ (\ Cos \ alpha = \ mare \ frac \ normalsize \) \ (\ cos \ beta = \ mare \ frac \ normalsize \)
Tangenta unghiului ascuțit este egal cu raportul dintre piciorul opus unui picior adiacent:
\ (\ Tan \ alpha = \ mare \ frac \ normalsize \) \ (\ tan \ beta = \ mare \ frac \ normalsize \)
unghi ascuțit cotangentă este egal cu raportul dintre piciorul adiacent unei catete opuse:
\ (\ Cot \ alpha = \ mare \ frac \ normalsize \) \ (\ cot \ beta = \ mare \ frac \ normalsize \)
Secant unghi ascuțit egal cu raportul dintre ipotenuzei cu piciorul adiacent:
\ (\ Sec \ alpha = \ mare \ frac \ normalsize \) \ (\ sec \ beta = \ mare \ frac \ normalsize \)
unghi ascuțit cosecant egal cu raportul dintre ipotenuzei la un opus:
\ (\ Csc \ alpha = \ mare \ frac \ normalsize \) \ (\ csc \ beta = \ mare \ frac \ normalsize \)
Teorema lui Pitagora
Suma pătratelor picioarelor este egală cu pătratul ipotenuzei:
\ (+ = \)
\ (= Fc \), \ (= gc \),
unde \ (f \) și \ (g \) - proiecții, respectiv, picioarele \ (a \) și \ (b \) pe ipotenuza \ (c \).
unde \ (h \) - înălțime trase din perpendiculară pe ipotenuza \ (c \) și \ (f \) și \ (g \) - proiecții, respectiv, picioarele \ (a \) și \ (b \) ipotenuzei.
Valoarea mediană a dus la picioarele unui triunghi dreptunghic
\ (M_a ^ 2 = - \ mare \ frac >> \ normalsize \) \ (m_b ^ 2 = - \ mare \ frac >> \ normalsize \),
în cazul în care \ (\) și \ (\) - mediană a scăzut pe picioare \ (a \) și \ (b \).
Mediana atras ipotenuzei
\ (= \ Mare \ frac \ normalsize \), în cazul în care \ (\) - mediană a scăzut de la ipotenuza unghi drept \ (c \).
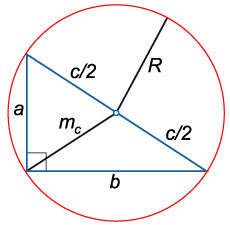
Raza cercului circumscris despre un triunghi dreptunghic
\ (R = \ mare \ frac \ normalsize = \)
Raza unui cerc înscris într-un triunghi dreptunghic
\ (R = \ mare \ frac> \ normalsize = \ mare \ frac >> \ normalsize \)
Suprafața unui triunghi dreptunghic
\ (S = \ mare \ frac> \ normalsize = \ mare \ frac> \ normalsize \)