Triple integrale, și exemple de formula
Conceptul triplei integralei administrat analog cu conceptul de dublu integrală.
Să presupunem că funcția definită într-o regiune închisă mărginită care aparține unui anumit spațiu tridimensional cu sistemul de coordonate carteziene. Vom împărți regiunea predeterminată pe părțile care nu au puncte comune și volume interne, care sunt respectiv egale. În fiecare regiune elementară să ia un punct arbitrar și formează suma, numită suma integrală pentru funcția de regiune.
Să - cea mai mare distanța dintre punctul de unitatea de suprafață. Dacă există o limită care nu depinde de metoda de partiționare câmpului în zone elementare sau prin selectarea acestora în puncte, această limită se numește o triplă integrală a câmpului, și se notează
Să - închis regiunea spațială, care este delimitată de suprafețele de sus și de jos, respectiv, și () și o latură - suprafață cilindrică având generatoarele paralele cu axa (figura 1.).
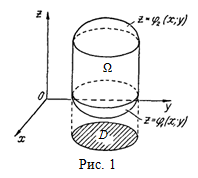
Variabile și schimbarea într-o regiune plană, care este o proiecție a unei regiuni spațiale pe un plan de coordonate.
Carteziană coordonate elementul de volum sistem este calculat conform formulei. Pentru o triplă integrală a regiunii a spus este:
Integrala interior este calculată în variabila, iar variabilele în acest caz, presupusă constantă. Rezultatul integrării este o funcție de variabile, și -. Astfel, calculul triplu integrale reduce la calcularea dublei integralei.
Ordinea integrării în triplă integrala poate fi schimbată, care este, interior integrala poate fi atât variabilă și variabila.