Teorema și determinarea geometriei (clasa 2), povestiri
Obținerea de-a doua lecție de studiu dedicat Teoreme axiome și definiții clasa 7 geometrie.
25. PROPRIETATE perpendicular pe linia - este o definiție complexă, care este de 4 ori mai mare decât cuvântul „dat acest lucru,“ și nici unul dintre ei să fie ratat. Am citit dintr-un anumit punct, care se află pe o anumită linie ACESTEA înainte în această semiplanului POATE FI DOAR UNUL se va ridica perpendiculara.
26. bisectoarea - jumătate de linie, care provine de la colțul de sus și bisects unghi.
- în cazul în care cele două părți și un unghi. cuprins între un triunghi sunt egale cu două laturi și unghiul făcut între ele, celălalt triunghi, atunci triunghiuri sunt egale;
- în cazul în care două laterale adiacente și la acesta un unghi al triunghiului, sunt, respectiv, lateral și un adiacent acesteia alte două colțuri ale triunghiului, aceste triunghiuri sunt egale;
- În cazul în care trei laturi ale unui triunghi sunt egale cu cele trei laturi ale unui alt triunghi, atunci triunghiuri sunt egale.
Corolar. În triunghiuri egale față laturile egale sunt unghiuri egale și împotriva unghiurile egale sunt laturile egale.
28. Mediana - un segment care leagă vârful triunghiului cu punctul de mijloc partea opusă.
29. Triunghiul bisectoarei - un bisectoare segment al unghiului triunghiului cuprins între partea superioară și partea opusă. În bisectoare are un început, dar fără sfârșit, iar la bisectoarea triunghiului este începutul este sfârșitul.
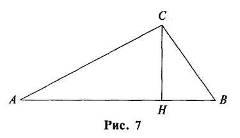
- înălțimea triunghiului - este perpendiculară a scăzut de la vârful triunghiului la
partea opusă sau continuarea acesteia;
- este perpendiculară a scăzut de la vârful triunghiului la linia care conține partea opusă.
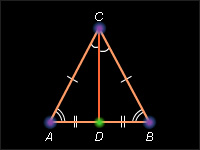
- triunghi isoscel - un triunghi în care cele două părți sunt egale.
Proprietatea - într-un triunghi echilateral, unghiurile de la baza sunt egale.
32. Proprietatea de un triunghi isoscel medianele:
- unghiul median la vârful unui triunghi isoscel este, de asemenea, bisectoarea și altitudinea.
33. Proprietatea celor două linii drepte paralele cu a treia:
- Dacă două linii paralele în afară de una și aceeași treia, atunci ele sunt paralele între ele.
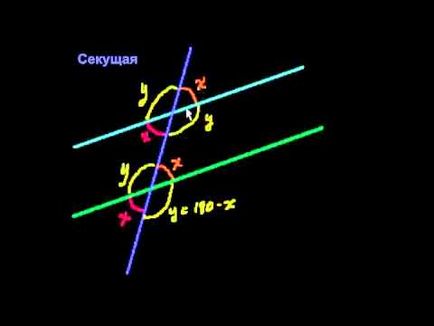
- la intersecția a două linii drepte formate de-a treia pereche de o singură parte patru colțuri, patru perechi mint unghiuri în lățime și 4 perechi de unghiuri corespunzătoare.
35. Semnele de linii paralele:
- în cazul în care, la intersecția a două drepte treia pare că unghiurile situate orice cruce sunt egale sau unghiuri corespunzătoare sunt egale, sau orice unilateral adăuga până la 180 de grade, atunci aceste linii sunt paralele.
36. Proprietatea este situată transversal, respectiv, și colțurile unei fețe:
- Dacă două linii paralele sunt traversate de un al treilea, unghiurile transversale situate sunt egale, unghiurile corespunzătoare sunt colțuri egale și o singură față, în valoare egală cu 180 °.
consecinţe:
- într-un triunghi echilateral, toate unghiurile sunt egale cu 60 °;
- într-un triunghi dreptunghic este egal cu suma unghiurilor acute de 90 °;
- un triunghi isoscel unghi-dreapta sunt unghiuri acute de 45 °;
- într-un picior drept triunghi culcat împotriva unghi de 30 °, egală cu jumătate
ipotenuza;
- Unghiul exterior al triunghiului este egală cu suma dintre cele două colțuri interioare nu sunt adiacente ei:
- Dacă două unghiuri ale unui triunghi sunt egale cu două unghiuri ale unui alt triunghi, apoi terța unghiurile acestea sunt.
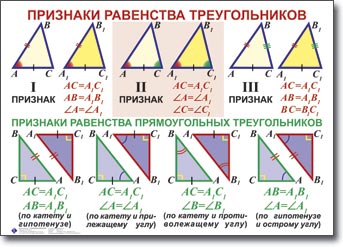
1. în cazul în care picioarele triunghiului, respectiv, egală cu un picior al unui alt triunghi, atunci triunghiuri sunt egale;
2. în cazul în care piciorul adiacent la aceasta, și unghiul ascuțit al triunghiului sunt egale, respectiv, la un picior și un unghi ascuțit adiacent la acesta a unui alt triunghi, aceste triunghiuri sunt egale;
3. Dacă catete la acesta opus și un unghi ascuțit al triunghiului sunt egale, respectiv, la un picior și un unghi ascuțit opus acestuia alt triunghi, aceste triunghiuri sunt egale;
4. dacă ipotenuză și un unghi ascuțit al triunghiului și ipotenuza, respectiv, egal cu unghiul ascuțit al celuilalt triunghi, aceste triunghiuri sunt egale;
5. În cazul în care ipotenuza și piciorul unui triunghi sunt egale cu ipotenuzei și un picior al unui alt triunghi, atunci triunghiuri sunt egale.
39. Teorema pe unicitatea perpendiculara a scăzut:
- dintr-un punct în afara liniei pe linie, puteți plasa perpendicular și numai unul.
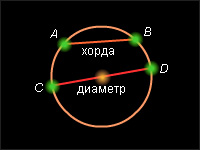
- cerc - curba închisă pe un plan ale cărui puncte sunt echidistante față de centrul cercului;
- cerc - a planului delimitat de un cerc;
- coardă - un segment care conectează două puncte ale circumferinței;
- diametru - coardă care trece prin centrul cercului;
- raza - segment de legătură pentru un punct central de pe circumferință;
- arc - o parte a circumferinței;
- sector - o parte a unui cerc, închis între două raze și un arc de cerc;
- segment - o parte a cercului, închise între coardă și arc.
41. locul geometric al punctelor (HMT) - toate punctele planului sau spațiu,
care au aceleași proprietăți.
cruce cercul.
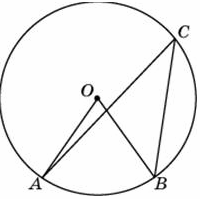
43. Unghiul inscripționată și măsurarea lui.
- unghiul inclus - unghiul vârful care se află pe un cerc, iar laturile se intersectează cercul;
- unghiul inscripționată este măsurat cu o jumătate de arc pe care se bazează;
- unghiul inclus egal cu jumătate din centru, laturile care trec prin același punct al circumferinței și că latura unghi circumferențial, și dacă un anumit unghi inscris este obtuz, completează jumătatea centrală la 180 °.
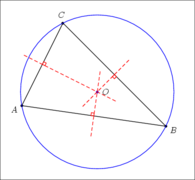
- trei intersectează perpendicular pe mediană, la un singur punct, iar acest punct este centrul cercului.
45. Al doilea centru Triangle:
- trei Bisectoarele unghiuri ale unui triunghi se intersectează într-un punct, iar acest punct
Acesta este centrul cercului înscris.
Lecția 1 Tutorial 3