Soluție grafică a ecuațiilor pătratice

Soluție grafică a ecuațiilor pătratice

Cu ecuații pătratice ați întâlnit deja în curs de algebra în clasa a 7-a. Să ne amintim că o ecuație pătratică este numită o ecuație de forma ax 2 + bx + c = 0 unde a, b, c - orice numere (raporturi), în care un. Folosind cunoștințele noastre despre unele dintre funcțiile și graficele lor, suntem capabili să chiar și acum, fără să mai aștepte pentru studiul sistematic al temei „ecuațiilor de gradul doi“ (acest lucru va fi mai târziu, în capitolul 4), pentru a rezolva unele ecuații pătratice, și în diferite moduri; Considerăm că aceste metode pe exemplul unei ecuații pătratice.

Exemplu. Pentru a rezolva ecuația x 2 - 2x - 3 = 0.
Decizie.
Metoda I. Se trasează functia y = x 2 - 2x - 3, folosind algoritmul lui § 13:

1) avem = 1, b = -2, x0 = 1, y0 = f (1) = 1 cu 2 - 2 - 3 = -4. Prin urmare, vârful parabolei este un punct (1, 4) și axa parabolei - Linia dreaptă x = 1.

2) să ia pe axa x două puncte simetrice în raport cu axa parabole, de exemplu x = -1 și x = 3.

3) După punctul (-1, 0), (1, -4), (3, 0) efectuarea parabolei (a se vedea figura 68) ..

Rădăcinile ecuației x 2 - 2x - 3 = 0 este abscisa punctelor parabolei de intersecție cu axa x; înseamnă rădăcinile ecuației sunt x1 = - 1, x 2 - 3,.

Metoda II. Noi transformam ecuatia la forma x 2 = 2x + 3. Construit în una grafică de coordonate funcții de sistem y - x 2 și y = 2x + 3 (Figura 69.). Ele se intersectează în două puncte A (- 1, 1) și B (3, 9). Rădăcinile ecuației sunt abscisele punctelor A și B, apoi x1 = - 1, x 2 - 3.

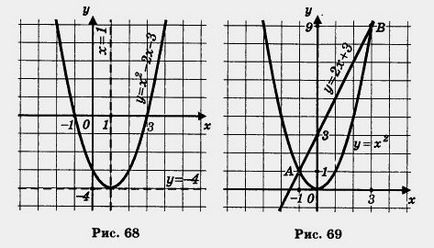
proces III. Noi transformam ecuatia la forma x 2 - 3, = 2x. Construindu funcționarea respectivului sistem de coordonate grafice y = x 2 - 3, și y = 2 (Figura 70.). Ele se intersectează în două puncte A (-1, - 2) și B (3, 6). Sunt rădăcinile punctelor abscisă A și B, totuși = x1 - 1, x2 = 3.

Metoda IV. Transforma ecuația în x 2 -2x 4-1-4 = 0
și în continuare
x 2 - 2x + 1 = 4, adică, (x - .. IJ = 4.
Construim într-un singur sistem de coordonate, parabolei y = (x - 1) 2 și linia y = 4 (Figura 71.). Ele se intersectează în două puncte A (-1, 4) și B (3, 4). Rădăcinile ecuației sunt abscisele punctelor A și B, prin urmare, x1 = -1, x2 = 3.

Metoda V. Termwise Împărțind ambele părți de x, obținem

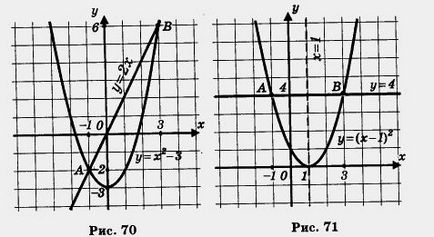
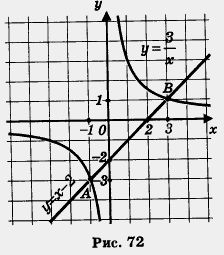
Construim într-un singur sistem de coordonate, o hiperbolă și o linie dreaptă y = x - 2 (Fig 72.).

Ele se intersectează în două puncte A (-1, -3) și B (3, 1). Sunt rădăcinile punctelor abscisă A și B, prin urmare, x1 = - 1, x2 = 3.

Deci, ecuația de gradul doi x 2 - 2x - 3 = 0, am decis să grafic cinci moduri. Să analizăm ceea ce este esența acestor metode.

Metoda I. Funcția complotat la punctul de intersecție cu axa x.

Metoda II. Conversia ecuația pentru a forma axa 2 = -BH - pentru a construi parabolei y = ax 2 și linia y = -BH - pentru a găsi punctul lor de intersecție (rădăcini ale ecuației sunt abscisele punctelor de intersecție, desigur, dacă este cazul).

proces III. Ecuația este convertit la forma ax 2 + c = - bx build parabolei y - ax 2 + c și linia y = -BH (ea trece prin origine); găsi punctul de intersecție.

Metoda IV. Aplicând metoda de alocare a unui pătrat perfect este transformat în forma ecuației

și (x + l) 2 + m = O
și în continuare
și (x + I) = - m

Build parabole y = a (x + I) 2, iar linia y = - m, paralelă cu axa x; găsi punctul de intersecție al unei parabole și o linie dreaptă.

Metoda V. Conversia ecuația formei

Build hiperbolă (aceasta - hiperbolă, cu condiția ca) și linia dreaptă y = - ax - b; găsi punctul de intersecție.

Rețineți că primele patru moduri sunt aplicabile la oricare din ecuațiile de forma ax 2 + bx + c = 0, cinci - doar cele în care p. În practică, puteți alege modul în care credeți că cel mai potrivit pentru o anumită ecuație, sau pe care le place (sau să înțeleagă).

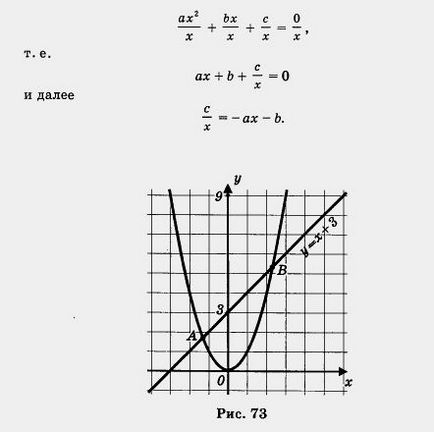
Notă. În ciuda abundenței de metode de soluții grafice de ecuații pătratice, încrederea în faptul că orice ecuație pătratică putem rezolva grafic, nr. Să presupunem, de exemplu, este necesar să se rezolve ecuația x 2 - x - 3 = 0 (ia în mod specific ecuația care este similar cu ceea ce a fost discutat în exemplu). Încearcă să-l rezolve, de exemplu, a doua metodă: transformă ecuația în x 2 = x 3 + construct parabolei y = 2 și
linia y = x + 3, ele se intersectează în punctele A și B (fig. 73), atunci ecuația are două rădăcini. Dar ce sunt acele rădăcini, nu putem spune desenul - punctul A și B nu sunt la fel de poziție „bun“, la fel ca în exemplul de mai sus. Acum, ia în considerare ecuația x 2-95 = 0. 16h- încercați să-l rezolve, de exemplu, a treia metodă. Noi transformam ecuatia la forma x 2-95 = 16x. Aici este necesar pentru a construi y = x parabolei 2-95, și linia y = 16x. Dar foaia de dimensiuni limitate de notebook-uri nu permit să facă, pentru că parabolei y = x 2 ar trebui să fie redus la 95 de celule în jos.

Deci, soluții grafice la frumos și plăcut ecuația de gradul doi, dar nu oferă o garanție absolută a soluțiilor de orice ecuație pătratică. Vom lua în considerare, • altele.

Matematica descărcare. elev sarcină 8 materiale de clasă în matematică pentru clasa a 8 on-line

Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.

Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.