Integrale triple - studopediya
3.1. Definiția triplu integrale
integral Triple este complet analog dublu integral. Să presupunem că într-o regiune tridimensională (V) o funcție continuă de trei variabile.
Impartim regiunea (V) într-un mod arbitrar pe regiunile n elementare (Vi) (i = 1,2 ... n), fără puncte interioare comune care sunt notate în volum.
Am ales în fiecare din punct arbitrar și formează suma integrală
Vom nota cu # 955; cel mai mare diametru al regiunilor elementare (V1), (V2) .... (Vn) :. în cazul în care.
În cazul în care limita atunci când suma integrală # 955; → 0 (n → ∞), care este independentă de orice metodă de partiționare câmpului (V) naelementarnye regiunea și selectarea punctelor din fiecare regiune elementară, această limită se numește o integrală triplă a regiunii (V), și reprezintă funcții:
Funcția în acest caz se numește integrabile în (V).
Notă. Proprietăți integralelor triple complet analoage cu proprietățile integralelor duble.
3.2. Calculul integralelor triple
3.2.1. Calculul integralei triple în coordonate rectangulare
Să - continuu în funcțiune (V), (V) - o parte a spațiului delimitat de suprafața superioară. și de jos - suprafața.
Fie (D) - proiecția (V) la planul Oxy.
Zona de delimitare (D) «sus» este un grafic al funcției. „Bottom“ - graficul functiei.
Zona de proiecție (D) pe axa Ox este segmentul [a, b] (fig. 14)
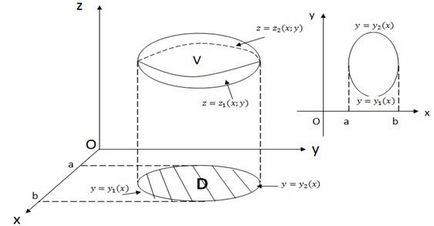
Apoi, avem formula:
Se calculează,
în cazul în care (V) - zona delimitată de planele x = 0, y = 0, z = 0, x + y + z = 1.
Soluție Zona (V) este prezentată în figura (15). prin urmare
Prin calcule simple, puteți veni la răspunsul.
Notă. În cazul în care.
în care - regiunea de volum (V).
3.2.2. integrant triplă în coordonate cilindrice.
punctul M proiecția pe planul Oxy și z applicate punctului M, adică (Figura 15.) - într-un sistem cilindric, poziția punctului M a spațiului definit prin coordonatele polare r și un punct de coordonate.
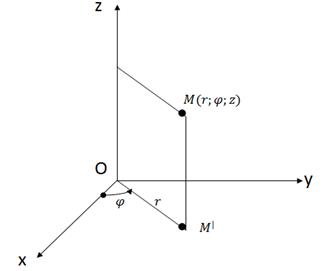
Numerele r, # 966;, z se numește coordonatele cilindrice ale punctului M.
Când se schimbă într-un sistem de coordonate cilindric este egal cu elementul de volum. tranziție r Jacobian.
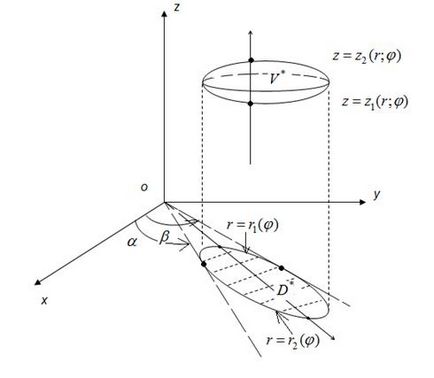
Apoi, următoarea formulă
EXEMPLUL Găsiți cilindru de volum de înălțime H și R. raza bazei
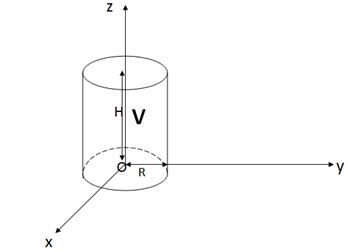
3.2.3. integrant triplă în coordonate sferice.
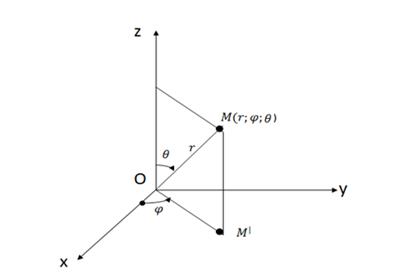
Într-un sistem sferic, poziția punctului M în spațiul definit de distanța r de la punctul M la sistemul de coordonate, un unghi de coordonate polare # 966; între direcția pozitivă a axei Ox și proiecția vectorului raza punctului M în planul Oxy un unghi și # 952; între direcția pozitivă a axei Oz și vectorul raza punctului M (fig. 18).
Numerele r, # 966;, # 952; numitele coordonate sferice ale punctului M.
Când se schimbă într-un sistem de coordonate cilindric este egal cu elementul de volum. Jacobi tranziției.
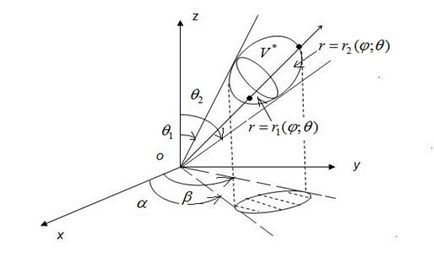
Apoi, următoarea formulă:
EXEMPLU Găsiți volumul unei sfere de rază R.
Soluția descrie mingea în sistemul de coordonate Oxyz (fig. 20).