geometria Axiom și efectul lor
Geometrie - știința formelor spațiale și a caracteristicilor cantitative ale obiectelor din lumea reală.
Geometria de construcții ca știință constă în selectarea conceptelor geometrice de bază, proprietățile de bază ale formulării acestor concepte geometrice, prin afirmații care sunt adevărate fără construcție dovezi și alte concepte. Această construcție se numește axiomatica.
Axioma - această afirmație este adoptat ca fiind adevărată, fără dovezi.
Se poate considera geometria avionului și în spațiu. Geometria planului se numește o planimetrie în spațiu - stereometrie.
concepte sau nedetectabile de bază sunt punctul planimetrie. drepte, și în geometria solidă - punct, linie și avionul.
Axiomele geometrie de bază
geometria axiomă pot fi împărțite în cinci grupe.
1. Accesorii axiome
1.1 Indiferent de drept, există puncte care îi aparțin și nu fac parte din ea.
1.2 prin orice două puncte, poți desena una dreaptă și numai unul.
1.3 Oricare ar fi planul, există puncte care aparțin acestui plan, și puncte care nu îi aparțin.
2. Axiome locație
2.1 Dintre cele trei puncte pe linie, unul și numai unul se află între celelalte două.
2.2 Direct împarte planul în două jumătăți de avioane.
2.3 Dacă două linii distincte au un punct comun, care prin ele poti desena un avion și, în plus, doar unul.
2.4 Dacă două planuri diferite au un punct comun, atunci ele se intersectează într-o linie dreaptă care trece prin acest punct.
3. axiome de măsurare
3.1 Fiecare segment are o anumită lungime mai mare decât zero. Lungimea segmentului egală cu suma lungimilor pieselor în care se rupe sau orice punct.
Fiecare unghi de 3,2 grade are o oarecare măsură mai mare decât zero. Unghiul extins este. Gradul de măsură un unghi egal cu gradul suma unghiurilor de măsuri pentru care este întreruptă de o trecere rază între părți.
4. Axiome rafturi.
4.1 În orice jumătate din punctul său inițial al segmentului poate fi amânată o lungime predeterminată și numai unul.
4.2 Din fiecare jumătate jumătate plan într-un unghi predeterminat poate fi întârziată cu o măsură de grad predeterminat la unul și numai unul.
4.3 Indiferent de triunghi, există un triunghi este egal cu acesta, într-o locație prestabilită în raport cu această jumătate de linie.
5. Axioma de paralelism.
5.1 Printr-un punct nu pe o anumită linie poate deține mai mult de o linie paralelă cu acest lucru.
Exemple de rezolvare a problemelor
Două avioane și se intersectează într-o linie dreaptă. Directă și transversală. În cazul în care este punctul de intersecție al liniilor și?
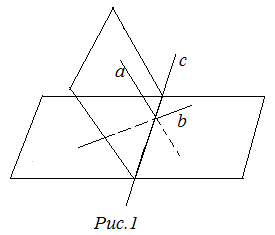
Dacă două planuri se intersectează într-o linie dreaptă, atunci toate punctele care linia aparțin atât primul și al doilea plan. Deoarece calea cea dreaptă se află în planuri diferite și, astfel, se intersectează, atunci punctul lor de intersecție aparține ambelor planuri și, în mod evident, se află pe linia.
Punctul de intersecție a liniilor drepte și este situat pe linia.
Determina un număr maxim posibil de avioane pot fi trase prin fasciculul de date 3 cu un punct inițial totală (nu există două grinzi se află pe o linie dreaptă)?
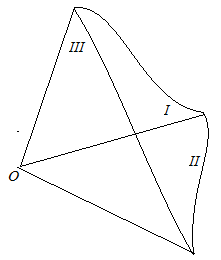
Conform axiomei 2.3 prin orice două linii cu un punct comun poate fi realizat singur plan. Prin urmare, în cazul în care trei grinzi nu se află în același plan, acestea pot fi împărțite în trei perechi diferite de raze. Apoi, numărul maxim posibil de avioane, care poate transporta este de trei.
3 maxim fascicul de date pe care le puteți petrece trei avioane.