Determinarea factorului de similaritate - folosesc triunghiuri similare pentru a rezolva probleme practice,

Prin urmare, similar, de exemplu, iar ortotreugolnikortotreugolnika triunghiul original ca triunghiuri cu laturile paralele. Astfel, aceste triunghiuri sunt similare, deoarece ambele isoscel cu unghiuri egale de la baza (adică pe cele două colțuri).
Koeffitsientpodobiya exprimă proporționalitate, raportul dintre lungimile laturilor un triunghi sunt congruente cu cealaltă: k = AB / A'b „= BC / B'C“ = AC / A'C“. laturile congruente în triunghiuri sunt opuse unghiurile egale. Koeffitsientpodobiya pot fi găsite în multe feluri.
Deoarece triunghiurile sunt similare pentru condiție, găsi-le laturile congruente. Găsiți raportul dintre laturile congruente, care va fi raportul similaritate. Una dintre proprietățile de triunghiuri similare, afirmă că raportul dintre zonele lor este egală cu pătratul factorului de similaritate. Se împarte valorile zonelor acestor triunghiuri una față de cealaltă și având rădăcina pătrată a rezultatului.
Dacă vom împărți lungimea sau înălțimea Bisectoarele trase din același unghi, veți obține, de asemenea, un coeficient de similaritate. Prin teorema lui sinus pentru orice relație triunghi dintre părțile la Sines unghiurilor opuse sunt egale cu diametrul unui cerc desenat în jurul acestuia. Utilizați aceeași cale pentru a găsi coeficientul, dacă ați introdus în cercul triunghiuri similare cu rază cunoscută.

Cum de a găsi raportul similaritate de triunghiuri
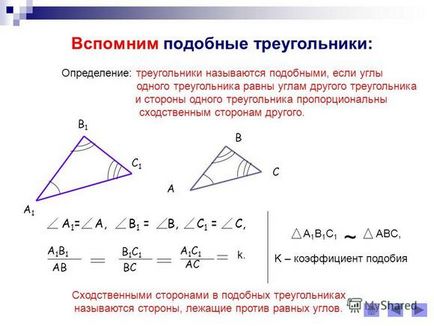
În practică, pentru stabilirea unor triunghiuri similare suficient pentru a verifica unele (vezi. Fig. 1). Combinații ale acestor ecuații sunt numite semne de similitudine de triunghiuri. Astfel, semnele de triunghiuri similare - o semne geometrice care permit să se stabilească faptul că cele două triunghiuri sunt similare, fără utilizarea tuturor elementelor. Similaritatea Coeficientul k este egal cu raportul dintre dimensiunile liniare corespunzătoare F și forme pătrate, prin urmare, cum ar fi pătrate forme includ dimensiunile liniare corespunzătoare.
13.4. Domenii de cifre similare
Aceste triunghiuri sunt identificate după cum urmează: Δ ABC
Δ A1B1C1. A = A1, B = B1, C = C1 și AB / a1b1 = Bc / AC = V1C1 / A1C1 = k, unde k - coeficientul de similaritate.

Similaritatea în triunghiuri dreptunghiulare.
Nota 3: Aceste cerințe sunt enumerate în definiția de triunghiuri similare sunt redundante. Aceste elemente de triunghiuri similare sunt cele care sunt măsurate în unități de lungime. Este, de exemplu, latura triunghiului, perimetrul median. Cerințe care se aplică definiției triunghiuri similare (este unghiuri egale și laturile proporționale) sunt redundante.
Pompă centrifugă legile afinității. coeficient de viteză.
Teorema pe intervale proporționale dovedit în mod similar cu teorema lui Thales (numai în loc de triunghiuri egale de similaritate utilizate aici). În cazul în care cea mai mică dintre cele două bucăți de date conținute într-un număr întreg mai mare de ori, segmentul mai mic și este cea mai comună de măsură a acestor două segmente. Raportul este raportul dintre cele două segmente ale lungimii lor, exprimate în aceleași unități.
Mediana - un segment care leagă oricare vârf al triunghiului la punctul median al laturii opuse. Acest punct se numește centrul de greutate al triunghiului. Această parte se numește baza triunghiului. Segmentul de bază care unește acute tăieturi înălțimi triunghi din acest triunghi similar cu acesta din factorul de similaritate egal cu cosinusul unghiului total al acestor triunghiuri.
Într-un triunghi-acută, înălțime două triunghiuri similare sale tăiat de la el. In triunghiuri similare linii (înălțimea medie bisector m. P.) corespunzătoare sunt proporționale. Mijlocul triunghiului este linia care leagă punctele mediane ale celor două părți. Pentru corpurile tridimensionale similare având un volum de teoremă similar are loc: raportul de volum al acestor organisme este egal cu cubul coeficientului de similaritate.
Lecția Subiect: „Primul semn de similitudine de triunghiuri.“ clasa a 8-a
Exemple de aplicații ale acestei investigații, a se vedea mai jos, a se vedea :. „Exemple de triunghiuri similare“ și „Proprietăți de paralelism (antiparalele) legate de triunghiuri părți“. Dreptunghi nu poate fi similar cu triunghiul.
De exemplu, în sarcina sunt triunghiuri similare și având în vedere lungimea laturilor lor. Pentru a face acest lucru, scrie în jos lungimile laturilor una și cealaltă în ordine crescătoare. Puteți calcula factorul podobiyatreugolnikov dacă știi zona lor.
Înălțimea triunghiului
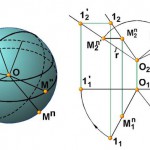
Utilizați această proprietate pentru a găsi coeficientul, în cazul în care aceste valori sunt supuse problemei. Fig. 2 arată că, în triunghiuri similare proporții egale, și diferă numai în scară. Pentru a stabili similitudinea triunghiuri poate fi și mai puține elemente.
Cele trei AD triunghi medianele, CF, BE se intersectează la un moment dat O, întotdeauna situată în interiorul triunghiului și este centrul de greutate. perimetrelor Relationship, lungimile medianele, mediatris construite pe laturile congruente sunt egale cu coeficientul de similitudine. Suprafața unui triunghi este egală cu jumătate din produsul din laturile și înălțimea. Prin urmare, toate medianele unui triunghi se intersectează într-un punct, împărțind fiecare dintre ele în raport cu 2. 1, pornind de la partea de sus.
A se vedea, de asemenea:
- România în epoca revoluțiilor palatului 1725-1762 bienal Consiliului Suprem Privy în 1731 a fost înlocuit Cabinetul de trei miniștri, în frunte cu AI Osterman. De 37 de ani de la moartea lui Petru I domniei lui Ecaterina a II (1725-1762) a ocupat tronul șase [...]

- Liniile de ecuații și curbe pe un formular plan plan de rescriere din care este clar că „Z“ poate lua orice valoare. 2. Pentru a aduce ecuatia la forma canonică și construi o curbă în sistemul inițial [...]
- Reforma Biserica lui Petru I Cazul a dus la Senat, iar Senatul achitat medicul. Și clerul în acest sens, au fost stabilite de către Petru responsabilitățile grave. La fel cum există, Petru a avut grijă de unitatea de supraveghere a [...]
