derivat on-line

Reguli de funcții de intrare.

1. Toate operațiunile matematice exprimate în termeni de simboluri convenționale (+, -, *, /, ^). De exemplu, x 2 + xy, scrise ca x ^ 2 + x * y. Sau, de exemplu, derivatul cosx + e + sinx x 3. scrise ca cos (x) + exp (sin (x) + x ^ 3).
2. Pătrat √ rădăcină¯ ≡ sqrt. De exemplu, sqrt (x ^ 2 + 1/2 * y ^ 2), e x = exp (x). Numărul π ≡ pi. păcatul 2 x ≡ sin (x) ^ 2, log5 (x) ≡ log (x, 5).

Împreună cu acest calculator folosesc, de asemenea, următoarele:

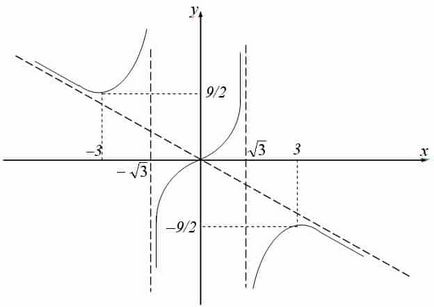
Metoda funcției Trasarea de calcul diferențial

Cum de a găsi derivat, bazat pe definiția acestuia.

Aplicații ale derivatului

Calculând derivata primului și al doilea ordin este folosit în multe aplicații. Luați în considerare cele mai comune.

1. Găsirea extremelor funcției unei singure variabile la zero este realizată prin echivalarea derivatului: f „(x) = 0. Acest pas este esențial pentru funcția de trasare de calcul diferențial.
2. Valoarea derivatului la punctul x0 permite să găsească ecuația tangentei graficului.
3. Atitudinea derivați ne permite de a calcula limitele statului L'Hopital lui.
4. În statistica matematică densitatea distribuției f (x) este definit ca derivata funcției F (x) de distribuție.
5. Atunci când caută o soluție particulară a ecuației diferențiale liniare necesare pentru a calcula derivata dintr-un punct.
6. In metoda lui Newton folosind derivatul este separat rădăcini de ecuații neliniare.