Cum de a găsi volumul unui cub versiune a problemei și soluția lor

Cum de a găsi elementele cubului de partea lui?

Deoarece linia modelează - un pătrat, aria va fi determinată prin formula №1, în care o cantitate cunoscută necesară pentru pătrat:

O diagonală a fiecărei fețe este calculat prin formula №2, care parte se înmulțește cu rădăcina 2:

formula anterioara derivată din teorema lui Pitagora. Este ușor de înțeles dacă vezi că fațetele diagonale - este ipotenuza unui triunghi dreptunghic. Și picioarele partea lui pătrat sunt.

Pentru a defini diagonala cubului, veți avea nevoie de următoarea formulă №3, care conține un anumit fel și rădăcina pătrată a 3:

Ea, de asemenea, este derivat din teorema lui Pitagora. La fel cum ipotenuza servește dorită diagonală. Picioarele sunt de aceeași parte a pătrat și diagonală.

Uneori este necesar să se cunoască formula de calcul aria suprafeței laterale a figurii. Acesta este înmulțită cu pătratul partea 4. Aici este (№4):

Înțelegeți cum să obțină această formulă, este ușor. Fețele laterale - 4. Aceasta înseamnă că suprafața totală a lor - de patru ori valoarea zonei de un pătrat.

Dacă doriți să determinați aria întregii suprafețe. apoi utilizați această înregistrare în care ushesteryaetsya nervură pătrat (Formula №5):

Se obține similar cu formula anterioară, numai numărul de pătrate a crescut la 6.

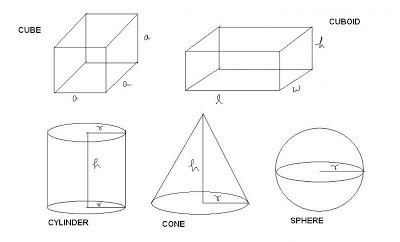
Care este volumul?

Pune pur și simplu, este un loc care ia orice corp în spațiu. Orice subiect este limitată în suprafețe de spațiu. Pot exista câteva, dar există cazuri în care doar unul. De exemplu, în cazul în care corpul - este o minge. Dar aceste suprafețe sunt închise în mod necesar. Spațiul care ocupă corpul geometric, și va fi capacitatea sa, sau volum.

volumul Units

Când este vorba de solide, cantitatea de unități va fi întotdeauna dimensiunea cub. De exemplu, metru, centimetru sau tocati km. Pentru lichide luate litri, care sunt exprimate printr-un decimetru cub. Dar, dacă acestea ocupă volume foarte mari, ele, de asemenea, măsurat în metri cubi. De exemplu, în cazul în care debitul de apă înregistrat în apartament este considerat în m 3. După cum se dovedește că este mai convenabil și mai ușor de numeric.

Metoda 1: Aflați volumul unui cub, în ​​cazul în care partea cunoscută

Aceasta este cea mai simplă metodă care vă va spune cum să găsească volumul unui cub. El este doar pentru a construi valoarea părții de gradul al treilea. Cu alte cuvinte, trebuie să multiplice partea de trei ori. Prin analogie cu un cuboid arbitrar atunci când a fost necesar pentru a se multiplica toate dimensiunile sale liniare. Formula este scris ca (№6):

Metoda 2: întreaga suprafață a cunoscut

În acest caz, este necesar să se împartă valoarea cunoscută pentru rădăcina pătrată 6. Din răspunsul intermediar și construi un număr de metri cubi. Dacă vom scrie această formulă, obținem următoarea (№7):

Metoda 3: cub feței diagonală este dat

Pentru a ști cum să calculeze volumul unui cub, caz în care trebuie să efectuați următorii pași. În primul rând, să construiască o anumită importanță în cub, iar apoi înmulțim cu rădăcina pătrată a 2 și se împarte la 4. Formula pentru această problemă (№8):

Această ecuație se obține după cum urmează: o anumită dimensiune, ar trebui să fie împărțită la rădăcina pătrată a doua. Apoi, numărul ridicat la puterea a treia. După efectuarea transformării obținute în numărătorul cub diagonală, iar numitorul 2√2. Matematica impune ca o caracteristică nu a fost irațional. Prin urmare, dispune de ea prin înmulțirea cu √2. Apoi numărătorul apare √2, iar numitorul este obținut 4.

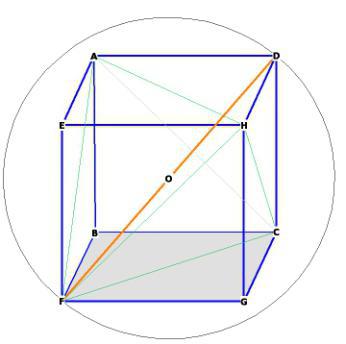
Metoda 4: cub diagonală

Formula care vă va spune cum să găsească volumul unui cub va conține pași: Cuadratura diagonală, înmulțirea cu rădăcina pătrată a 3, și împărțirea numai 9. Acesta va fi scris ca (№9):

Similar cu revendicările precedente, în primele intrări diagonale împărțit la rădăcina pătrată a trei și se ridică la cub. După schimbări în numitorul, de asemenea, apare irațional, de la care vrei să mergi. Deci, există o valoare în √3 numărător, și sub linia - 9.

exemple de sarcini

prima sarcină. Dan cub, cu o margine de 12 cm. Se calculează volumul și exprimă răspunsul în metri pătrați.

În această sarcină, aceasta va fi mai greu de a traduce răspunsul în alte unități, vă decide cum să găsească volumul unui cub. Pentru a efectua prima parte a sarcinii: Formula înregistrată cu numărul 6. După 12 cubul va răspunde la numărul de 1728 cm 3. Acum trebuie să ne amintim cum să le traducă în metri cubi. În acest scop, răspunsul ar trebui să fie împărțit în 100 de trei ori. O sută a venit de la faptul că un metru este de o sută de centimetri. O divizie se face de trei ori, deoarece unitatea cubul în loc de muncă. Deci, în 1728 împărțită la 100 va da 17.28. După cea de a doua divizie va 0.1728. Al treilea act va răspunde la 0.001728 m 3. Acesta este răspunsul la problema: volumul unui cub este egal cu 0.001728 m 3.

Al doilea obiectiv. Există un cub cu o suprafață de întreaga suprafață de 600 dm 2. Găsiți volumul cifrelor și să-l exprime în metri cubi.

Pentru a răspunde la întrebarea acestei sarcini va avea nevoie de un număr de formula 7. Prima acțiune a unui anumit număr este divizibil cu 6. Răspunsul devine 100. Din aceasta este ușor de a lua rădăcină pătrată, acesta va fi egal cu 10. Acum trebuie să construiască în zece metri cubi. Astfel, se obține că valoarea dorită este de 1000 dm 3. Rămâne să-l traducă în m 3. Ca și în problema de mai sus, divizia va fi efectuată de trei ori, doar separator va fi 10. Pentru că un metru zece decimeters. După împărțirea răspunsului obținut egal cu 1 m 3. A: volum egal de 1 m 3.

Al treilea obiectiv. Dan cub cu o lungime diagonală de fețele sale, egală cu √2 mm. Ai nevoie pentru a calcula volumul.

Formula a opta va ajuta în modul de a găsi răspunsul la această problemă. Primul pas este de a construi un cub într-o cantitate cunoscută. Rădăcina pătrată din 2 în al treilea grad va da valoare 2√2. După multiplicarea cu √2 obține numărul 4. Pasul final este necesar să-l împartă cu 4. Răspuns: Volumul unui cub de 1 mm3.

Al patrulea obiectiv. Este cunoscut faptul că diagonala cubului este egal cu 3 m. Este necesar să se calculeze volumul său.

Vor găsi doar răspunsul la această problemă, conform formulei de la numărul 9. Valoarea pe care este dată în condiție, este necesar să se construiască un cub. Turn 27. După divizarea în 9 va răspunde este 3. Și ultima acțiune trebuie să fie înmulțită cu rădăcina pătrată a 3. Sarcina de răspuns va 3√3 m3.