Ce este, prin urmare, în geometria 1

nu este un număr rațional, deoarece lungimile segmentelor | X1X2 | și | X1X3 | poate, în principiu, să fie exprimate prin numere iraționale. Cu toate acestea, în practică, nu are loc un astfel de eveniment. Pentru a determina lungimea segmentelor pe care le folosim întotdeauna orice dispozitiv de măsurare (cum ar fi un conducător de școală), care dă un rezultat rotunjite la o zecimală finită.

Să se dea linii divergente x și y. care se intersectează într-un punct O și mai mult - două linii paralele și n1 n2. linia x care se intersectează în punctele X1 și X2 și linia y la punctele Y1 și Y2. așa cum se arată în figură.

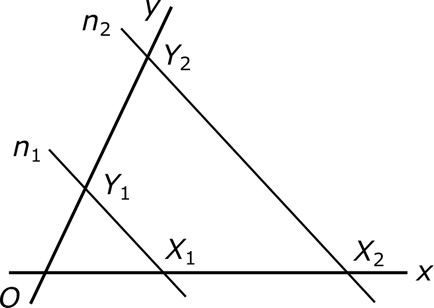
Apoi, liniile paralele și n1 n2. De fapt, atragem prin punctul X1 linie auxiliară paralelă cu linia n2. Prin teorema lui Thales generalizată, această linie auxiliară trece printr-un punct Y1. În consecință, aceasta coincide cu linia n1. Astfel, o paralelă directă cu linia n2 n1.

Mergem afară, luând foaia de hârtie și un creion. Nostru aranja orizontal foaia și a pus pe ea aproximativ în punctul central O. Din acest punct ține mental grinzi spre diferite puncte remarcabile ale terenului pe o rază de aproximativ o sută de metri - copaci, stâlpi, colțurile clădirilor și altele asemenea.

Să presupunem că avem o oportunitate de a măsura distanța față de aceste puncte notabile. Să presupunem, de exemplu, distanța până la cel mai apropiat copac este de 10 m. Mental amână de la punctul O în direcția segmentului de lemn, a cărei lungime este de 1000 de ori mai mică decât o distanță dată, și un creion pe poziție notă de hârtie al doilea capăt al acestuia. Este ușor pentru a calcula distanța de la punctul O la nivelul de 10 m / 1000 = 1 cm.

De asemenea, lăsați distanța până la un alt obiect remarcabil este x1. Înmulțiți această distanță de numărul k. egală cu 1/1000. amâna mental punctul O lungime de segment x2 = KX1 de-a lungul razei îndreptate la obiect. La punctul în lucrare în care celălalt capăt al segmentului, pentru a face un semn cu un creion. Vom efectua această procedură, cu toate punctele notabile pe teren, folosind tot timpul aceeași valoare a parametrului k. Dacă oricare dintre aceste puncte sunt interconectate printr-un gard sau un perete sau ceva similar, apoi între etichetele respective pe suport de hârtie și trage linie.

Ca urmare, această bucată de hârtie pentru a obține o locație hartă. Prin teorema lui Thales și proporția de proprietăți, toate relațiile dintre distanțele pe hârtie va fi exact la fel ca în realitate. Mai mult decât atât, toate liniile de pe hârtie va fi paralelă cu liniile corespunzătoare de pe teren. Această paralelă este, desigur, să fie rupt atunci când vom efectua lista noastră în altă parte, dar unghiurile dintre liniile rămân.

Parametrul k. pe care am folosit în construcția noastră, a numit un factor de scara, sau o scară. Desigur, nu trebuie să fie egal cu 1/1000. Se poate, în principiu, să aibă valoare, este important doar că această valoare a rămas neschimbată, în orice moment în timpul construcției hărții.

Pe aceste hărți scara trebuie să fie indicată în legendă, în același timp, în loc de slash este utilizat în mod obișnuit de colon. De exemplu, scara 1: 100.000 înseamnă că un centimetru pe hartă corespunde la 100.000 de centimetri (adică un kilometru) pe sol.

Desene tehnice sunt, de asemenea, întotdeauna rula, cum se spune, într-o anumită scară. Scara 1: 1 înseamnă că elementul este tras în mărime completă. O scară de 10: 1 spune că desenul făcut cu o creștere de zece ori.

Notă cu privire la liniile paralele

Noi am numit astfel drepte paralele nepotrivite, unghiul dintre ele este zero. Am observat că aceste linii nu se intersectează. Noi acum arată că în cazul în care liniile se află într-un plan și nu sunt paralele (adică, unghiul dintre ele este diferit de zero), atunci ei se vor intersecta undeva.

Lăsați avionul sunt două linii - x și n. Notă punct arbitrar pe ele - O și Y - și trage prin aceste puncte de-al treilea rând - y. Presupunând că unghiul dintre liniile x și n nu este zero, colțurile adiacente nu ar trebui să fie egale între ele. Pentru definiteness, să α1> α2. așa cum se arată în figură.

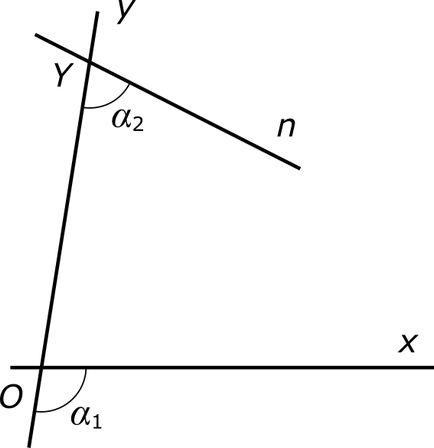
Prin punctul de linie O n1. paralel cu linia n. Trebuie remarcat pe ea de unghiul α1 punct arbitrar N1 și trage prin acest punct o linie dreaptă y1. paralel cu linia y. Aceasta formează un paralelogram, indicat în figura de fundal gri.

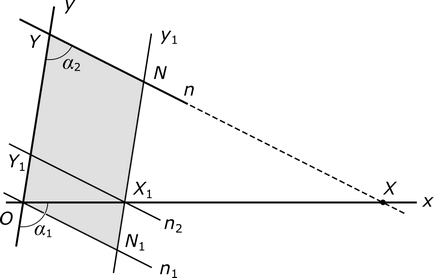
Acest lucru înseamnă că linia intersectează linia y1 n la un moment dat, pe care îl notăm cu N. Direct x. merge la „teritoriul“ al paralelogramului la O. neapărat undeva pentru a merge de acolo. Se poate face acest lucru fie prin YN segment. sau prin segmentul N1N. În primul caz, odată ce devine evident că linia x intersectează linia n. Luați în considerare al doilea caz. Notăm punctul de intersecție al liniei x și segmentul N1N prin X1. Prin n2 sale directe. paralel cu linia n. Această linie împarte paralelogram ON1NY în două noi paralelogram și intersectează linia y la un punct Y1. Notă privind linia x X. Acest punct care satisface relația

Desenați prin linia X și Y puncte. Așa cum sa discutat mai sus, corolarul teorema lui Thales, această linie este paralelă cu linia n2. și astfel formează un unghi de zero, cu linie dreaptă n. Prin urmare, o nouă linie coincide cu linia n. care se intersectează astfel linia x la punctul X.

Putem afirma acum că următoarele trei declarații pe liniile divergente a și b. coplanare, înseamnă exact același lucru:

(1) Unghiul dintre liniile a și b este zero.

(2) o directă și b nu se intersectează nicăieri.

(3) Drept a și b sunt paralele.

În curs de aprobare tradițională geometrie 2. paralelă directă este definiția am ales pentru această afirmație scop 1. Este mult mai ușor să se determine unghiul dintre două linii, decât să se asigure că nu se intersectează deloc întinderea sa infinită.

1. Egalitatea fel x1 / x2 = y1 / y2 se numește o proporție. Numărătorilor sunt proporționale cu numitor. Numărătorul și numitorul unei fracții sunt legate în același mod ca numărătorul și numitorul fracției cealaltă. Este echivalent cu: x1 / x2 = y1 / y2.

2. Teorema lui Thales generalizată. Să două linii arbitrare a și b se intersectează în trei linii paralele. Apoi, intercepta pe linia A. proporțională cu intercept corespunzătoare de pe linia b.

3. Corolar unghi lateral 1. Fie cu vârful în punctul O intersectează două linii paralele și n1 n2. Apoi intercepteaza pe liniile N1 și N2. Aceasta se referă la aceleași ca segmentele depuse pe fiecare parte a unghiului O din punct la punctele respective de intersecție cu n1 drepte și n2.

4. Corolar 2. Să o parte unghi întârziat din partea de sus a segmentelor, astfel încât segmentele pe de o parte proporțională cu celelalte segmente. Apoi, liniile care trec prin extremitățile respective ale acestor segmente, paralele între ele.

5. Harta stocate toate relațiile dintre distanțele și toate unghiurile. Raportul dintre cele două distanțe între anumite puncte de pe hartă la distanța dintre punctele corespunzătoare de pe teren nu depinde de alegerea punctelor numite scară.

6. În cazul în care unghiul dintre două linii drepte situate în același plan, nu este egal cu zero, atunci o astfel de directă se intersectează în mod necesar.