Care este limita de modul în care să-l găsiți

Conceptul Generalizat de o limită: există un număr limită de o anumită variabilă, în cazul în care în procesul de schimbare a valorii acestei variabile este infinit aproape de o.

Să ne explicăm acest lucru cu un exemplu, care ilustrează, de asemenea. După exemplu, să totale limitele algoritm soluție.

În plus, rezolvate în acest tutorial exemple și orice alte sarcini pe exterior, se poate verifica limitele calculator online.

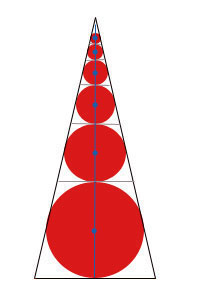
În partea de jos a unui triunghi isoscel inscripționată cerc. Diametrul cercului notat cu. Figura diametru conected albastru. Prin cercul paralel cu baza triunghiului tangentelor original (este cifra de gri). Rezultatul este un triunghi similar cu originalul. În acest triunghi se înscrie exact cerc. Diametrul său - (diametre ale figurii delimitate tangente). Construcții similare sunt în curs de desfășurare, permițând în același timp înălțimea triunghiului. Obținut cercuri succesiv mici și secvența corespunzătoare a lungimii diametrele lor. Această secvență de lungimi de diametre oferă un exemplu de o variabilă care crește cu un număr nelimitat circumferință x se apropie de zero. Limita acestei secvențe este zero :.

Să ne scrie exemplul dat în limba formulă. Deci, numărul de cerc crește și tinde la infinit, adică. Să presupunem există un triunghi isoscel, că lungimea diametrului fiecărui cerc înscris în acesta se calculează conform formulei

Valoarea pe care trebuie să găsim, vor fi înregistrate după cum urmează:

Lim acest lucru este limita, și a indicat variabilă sub ea, care tinde la o valoare certă - la zero, orice alt număr, infinit.

Acum vom calcula limita prin setarea variabilei x este infinit (în definiția strictă se numește „completează definiția funcției“, cu această definiție, se poate vedea capitolul „Limit“, în următoarele părți). Să presupunem că o cantitate finită împărțită la infinit este zero:

Deoarece secvența considerată a cercurilor asociază alte variabile - secvența sumei lor diametre:

Luând în considerare imaginea din nou, constatăm că limita a secvenței este egală cu h - înălțimea unui triunghi isoscel. În general, o limită poate fi zero, orice alt număr sau infinit.

Acum, definirea mai strictă a limitei funcției, pe care o puteți solicita la examen, precum și pentru înțelegerea care va necesita un pic mai multă atenție.

Să presupunem că funcția f (x) definită pe un set, și lăsați X să fie un punct. Ia-o secvență de puncte, altele decât X:

converge. Valorile funcției în punctele de secvență formează, de asemenea, o secvență numerică

și este posibil să se ridice problema existenței limita.

DEFINIȚIE 1. Un număr numit limita funcției f (x) la punctul (sau) în cazul în care pentru orice secvență converge la (1) valorile argumentului x. decât secvența corespunzătoare (2) converge la A.

Simbolic, este scris ca:

Asta înseamnă că: pentru a găsi limita funcției, este necesară pentru funcția x substitut valoarea solicitată de x.

Exemplul 1. Găsiți limita funcției la.

Decizie. Membru supleant x valoare în loc de 0. Obținem:

Astfel, limita funcției, atunci când este 1.

În plus, rezolvate în acest tutorial exemple, precum și orice alte sarcini pe exterior, este posibil să se verifice limitele calculator online.

Limita unei funcții la momentul și

Pe lângă luarea în considerare noțiunea de limită a unei funcții atunci când există, de asemenea, conceptul funcției limită atunci când argumentul tinde la infinit.

2. Determinarea numărului A se numește limita funcției f (x), atunci când, în cazul în care, pentru orice secvență infinită de (1) secvența corespunzătoare a valorilor de argument (2) al funcției converge A.

Simbolic, este scris ca.

Definiție 3. Un număr numit limita funcției f (x) la (), în cazul în care pentru orice secvență infinită de valori argument, elemente care sunt pozitive secvență (negativă) corespunzătoare (2) valorile funcției converge A.

Simbolic acest lucru este scris ca: ().

Acest lucru, la fel ca în cazul Definiție 1, înseamnă: pentru a găsi funcția de limită, trebuie să funcționeze pentru x infinit substitut, plus sau minus infinit infinit.

Exemplul 2. Găsiți limita funcției la.

Decizie. Substitut pentru x infinit. Că secvența funcției este infinitezimal, și, prin urmare, are o limită egală cu zero:

Pentru claritate și credibilitate atunci când se decide exemplul din proiect, puteți înlocui x numărul de superlarge. Veți obține numărul supersmall atunci când divizat.

Și a verifica afară soluția la limitele posibile limite pe calculator on-line.

Teorema 1. (o funcție în cadrul unei singure). Funcția nu poate avea mai mult de un punct.

Corolar. Dacă cele două funcții f (x) și g (x) sunt într-un cartier al punctului, cu excepția, poate, cel mai punct, sau ele sunt aceleași la limita, sau ambele nu au o limită în acest moment.

Teorema 2. Daca functia f (x) și g (x) au limite la punct, atunci:

1) să limiteze suma algebrică a funcțiilor este egală cu suma algebrică a limitelor termenilor, adică

2) Limita funcției produsului este produsul limitelor factorilor. și anume

3) limita raportul dintre două funcții este egală cu raportul dintre limita dividendului prin limita împărțitor dacă limita divizor nu este zero, adică

Notă. Formula (3) și (4) să dețină pentru orice număr finit de funcții.

Corolar constantă 1.Predel este foarte constantă. și anume

Factorul 2.Postoyanny de investigare poate fi luată ca un semn al limitei. și anume

Exemplul 3. Găsiți limită:

Și a verifica afară soluția la limitele posibile limite pe calculator on-line.

EXEMPLUL 4 Căutați limită:

Decizie. Asigurându-vă că împărțitor limită nu este egal cu zero:

Astfel, formula (5) se aplică, și, prin urmare,

Și a verifica afară soluția la limitele posibile limite pe calculator on-line.

Teorema 3 (la limita unei funcții compozite). În cazul în care există o limită finită

și funcția f (u) este continuă la un punct, atunci

Cu alte cuvinte, limita de simboluri și funcții funcții continue pot fi schimbate între ele.

aplicarea directă a teoremelor privind limitele, cu toate acestea, nu conduce întotdeauna la obiectivul. De exemplu, este imposibil să se aplice teorema limita privat, în cazul în care limita împărțitor este zero. În astfel de cazuri, trebuie să convertiți mai întâi funcția identică pentru a fi în măsură să aplice corolarul teoremei 1.

Exemplul 5. Găsiți limita:

Decizie. Teorema privind limita privat nu se aplică în acest caz, deoarece

Transformarea o fracție dată prin extinderea numărătorul și numitorul de factori. În numărătorul obținem

rădăcini ale trinomul pătratice (dacă ați uitat cum să rezolve ecuații pătratice, du-te aici). Acum am tăiat fracție și din corolarul teoremei 1, se calculează limita funcției:

Verificați soluția la limitele posibile limite pe calculator on-line.

La decizia din Exemplul 5, ne-am întâlnit deja greu de definit. Această incertitudine și incertitudinea de forma - cea mai comună incertitudinea pe care trebuie să le dezvăluie în abordarea limite.

O mulțime de probleme la exterior, devine elevii, transporta doar o astfel de incertitudine. Pentru divulgarea lor sau, mai precis, evitând incertitudinile, există mai multe metode de transformare artificială a formei de exprimare sub semnul limită. Aceste metode sunt după cum urmează: termen diviziunea numărătorul și numitorul de nivelul superior al variabilei, înmulțirea prin expresia conjugată și factoringului pentru reducerea ulterioară, folosind soluții de ecuații pătratice și formule de multiplicare prescurtate.

Maestru aceste tehnici cu exemple.

Pentru a converti expresii necesită acțiuni manuale cu puteri și rădăcini și operațiuni cu fracții.

Exemplul 6. Extindeți incertitudine, și pentru a găsi limita.

Decizie. Aici, cea mai mare putere a variabilei n este egal cu 2. Prin urmare, termenul de termen, împărțim numărătorul și numitorul:

Obținem răspunde la această limită la o funcție variabilă tinde la infinit egal.

Verificați soluția la limitele posibile limite pe calculator on-line.

Exemplul 7. Extindeți incertitudine, și pentru a găsi limita.

Decizie. Aici, cea mai mare putere a variabilei x este egal cu 1. Prin urmare, termenul de termen, împărțim numărătorul și numitorul de x:

Răspuns primit această funcție limită la o variabilă tinde la infinit este zero.

Verificați soluția la limitele posibile limite pe calculator on-line.

Exemplul 8. Extindeți incertitudine, și pentru a găsi limita.

Decizie. În numărătorul - diferența dintre cuburile. Am extinde la factorizarea, folosind formula de rata de multiplicare rezumative a matematicii școlare:

Scriem expresia, care rezultă din transformarea și să găsească limita de:

Verificați soluția la limitele posibile limite pe calculator on-line.

Exemplul 9. Extindeți incertitudine, și pentru a găsi limita

Decizie. Teorema privind limita privat nu se aplică în acest caz, deoarece

Prin urmare, identitatea transformă fracția: înmulțirea numărătorul și numitorul de numitorul conjugat binomială, și a scăzut cu x +1. Conform corolarul teoremei 1, obținem o expresie a decide care găsiți limita dorită:

Se verifică soluția la limitele posibile limite pe calculator on-line.

Exemplul 10. Extinderea incertitudine, și pentru a găsi limita

Decizie. substituție directă a valorii x = 0 într-o funcție predeterminată care duce la o incertitudine a formei 0/0. Pentru a-l dezvăluie, efectua transformări identice se va termina cu limita dorită:

Se verifică soluția la limitele posibile limite pe calculator on-line.