Calea traversat de organismul

Calea traversat de organismul sau mișcarea neuniformă din partea # 965; = f (t), intervalul de timp [t1, t2], este egal cu

corp 7.1.1.Dva a început să se miște în același timp, de la un singur punct într-o singură direcție într-o linie dreaptă. Un organism a fost în mișcare, la o viteză de m / s, iar celălalt la o viteză m / s.Na ce distanță sunt unul față de celălalt în 5 secunde?

Decizie. Conform formulei calculăm distanța parcursă primul și al doilea corp:

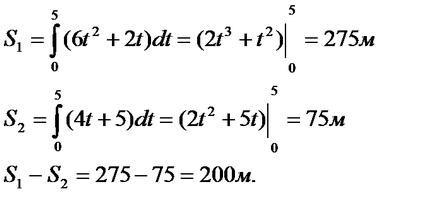
organismele 7.1.2.Dva muta într-o linie dreaptă de la același punct. Primul corp se deplasează la o viteză m / s. -CO a doua viteză .În ce moment și la ce distanță de punctul de plecare al reuniunii lor se va întâmpla?

Decizie. Condiția este dat sarcini pe care organismul a început să se deplaseze de la același punct, astfel încât căile lor va fi egală cu întâlniri USD. Să ne găsim ecuația calea fiecăruia dintre organismele

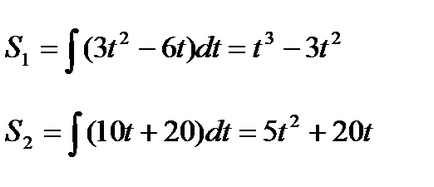
Constantele de integrare fără condiții inițiale sunt zero. Reuniunea acestor organisme se va întâmpla atunci când, în cazul în care

Noi rezolva această ecuație

La acel moment nu va fi o reuniune a acestor organisme după ce ne-am așezat în jos .Din ecuațiile de mișcare ale modului găsi

7.1.3. Corpul este aruncat de la sol pe verticală în sus, la o rată de .Nayti înălțime maximă de ridicare a corpului.

Decizie. Organismul atinge înălțimea maximă de ridicare la momentul t, atunci când # 965 = 0, adică.

39,2-9,8t = 0 la t = 4 secunde

7.1.4. Materialul se deplasează de-a lungul liniei drepte cu variabila SKO-creștere, care este o funcție de timp predeterminate t continuu: v = v (t). Determina calea parcursă de corp din momentul VRE Meni t0 la T. timp

Notă. Intervalul de timp [t0. T] n împărțit în porțiuni arbitrare. Lungimea fiecărui interval de timp

În fiecare perioadă de timp parțială vom alege un moment-ny arbitrar - # 964; k. (momentul # 964; k poate coincide cu oricare dintre capetele durata de timp # 8710; # 964; k).

Se calculează viteza v în acest moment. Ia un număr de f (# 964; k) acceptă că în timpul # 8710; # 964; mișcarea k este uniformă. Deoarece uniform rectilinie calea de mișcare viteza corp-proy denny este egal cu produsul din calea timpului proy-Denny în timpul # 8710; # 964; k. va fi aproximativ egal cu f (# 964; k) # 8710; # 964; k. Adăugați calea traversat pentru toate intervalele de timp parțiale.

Valoarea aproximativă a căii

Pentru valoarea exactă ar trebui să ia calea S-clorhidric Valoarea limită integrală (11,10), atunci când cele mai multe intervale de timp # 8710; tk tinde la zero:

Pe baza formulei (10.2) poate fi scris că

Astfel, dacă o anumită lege a schimbărilor de viteză, atunci calea parcursă de către organism, se calculează cu o formulă integrală-Grai predeterminate (11,11).

atunci când max # 8710; tk → 0, atunci produsul v (# 964; k) # 8710; # 964; k - valoare nu este infinit, infinit de mic. Determinarea cantității necesare și această problemă se reduce la găsirea limita suma infinit creșterea numărului de cantități infinit de mici.

7.1.5. Calculati calea traversata corp în cădere liberă în vid pentru T secunde dacă se știe că viteza v pas Denia liber în gol definit prin formula v = gt (V0 inițială de viteză accepta zero).

Răspuns. . Dacă v0 ≠ 0, atunci v = v0 + gt, un