Calea la mișcare neregulată

Acum vom lua în considerare mișcarea neregulată - adică, mișcarea în care valoarea absolută a modificării ratei de-a lungul timpului. Se pare că există o interpretare geometrică simplă a traseului parcurs de către organism, la o mișcare arbitrară.






Să începem cu o mișcare uniformă. Lăsați viteza corpului este constantă și egală. Să luăm două puncte în timp: punctul de pornire și se termină la punctul. Durata timpului de interval dat egal.

Este evident că, pentru perioada de timp corpul trece prin calea:

Să construim un grafic al vitezei în funcție de timp. În acest caz, va fi o linie dreaptă paralelă cu axa x (Fig. 1).

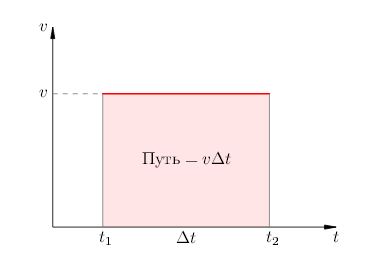
Fig. 1. Calea în mișcare uniformă

Este ușor de observat că distanța parcursă este egală cu suprafața dreptunghiului situată sub viteza graficului. De fapt, primul factor în ecuația (1) are o latură verticală a dreptunghiului, iar al doilea factor - partea sa orizontală.

Acum avem de a generaliza interpretarea geometrică în cazul mișcării neuniforme.

Să viteza corpului depinde de timpul și pe intervalul considerat Graficul de viteză arată astfel (figura 2):

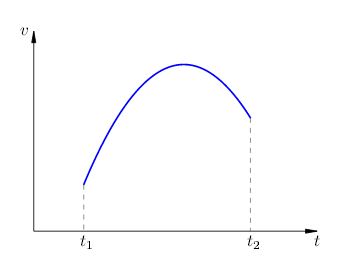
Fig. 2. mișcarea neuniforma

Apoi ne certăm după cum urmează.

1. Impartim perioada noastră de timp, în valoare de segmente mici.

2. Să presupunem că în fiecare organism astfel de segment se deplasează cu o viteză constantă. Adică, o schimbare lină a vitezei înlocui aproximării viteza *: pentru fiecare interval de timp mic corpului se mișcă uniform, iar apoi viteza corpului instantaneu și modificările ckachkom.
Fig. 3 prezintă două trepte de aproximare. Lățimea etapelor pe figura din dreapta mai puțin de jumătate din stânga.

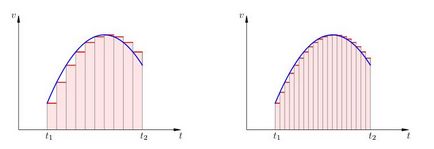
Fig. 3. Apropierea Stepped

Calea traversat în timpul mișcării uniform - zona dreptunghi este situată sub pasul. Prin urmare, calea de traversat pentru totdeauna o astfel de „trepte“ mișcare - este suma suprafețelor tuturor dreptunghiurile pe diagramă.

3. Acum tinde la zero. Este clar că viteza noastră va comuta apropierea limitei de viteză inițială în graficul din fig. 2. Suma zonele dreptunghiurile vor intra în zona de sub graficul vitezei; Prin urmare, această zonă este calea parcursă de corpul pentru un timp înainte. (Fig. 4

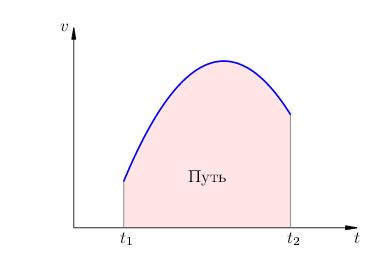
Fig. 4. Modul în mișcare neuniformă

Ca rezultat, am ajuns la noi dorit pentru a generaliza interpretarea geometrică a drum, obținut mai sus pentru cazul mișcării uniforme.

Apropierea - este înlocuirea aproximativă a unui obiect destul de complex, un model simplu, care este mai convenabil pentru studiu.

O interpretare geometrică a modului. Calea traversat de către organism în orice mișcare, egală cu aria de sub graficul vitezei, la un interval de timp predeterminat.

Să vedem cum această interpretare geometrică în importantul cazul special al mișcării uniform accelerate.

Sarcină. Un corp având o viteză în momentul inițial. Acesta accelerează cu accelerație constantă. Găsiți calea parcursă de corpul la un punct în timp.

Decizie. Dependența de timp a vitezei, în acest caz, are forma:

program rate - drepte, este prezentată în Fig. 5. Încercarea de modul în care există zona trapez situată sub viteza graficului.

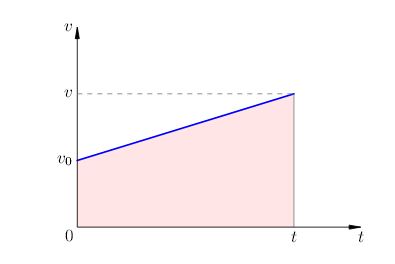
Fig. 5. Calea cu mișcare uniform accelerată

Baza mică a trapezului egală. terenuri mari de îngrijire. Înălțimea trapezului este egală. Având în vedere că aria unui trapez este produsul jumătății sumei de baze pe mare, avem:

Această formulă poate fi rescrisă sub forma mai familiar:

Ea, desigur, bine cunoscut pentru tine de la subiect „Uniform accelerat de mișcare.“

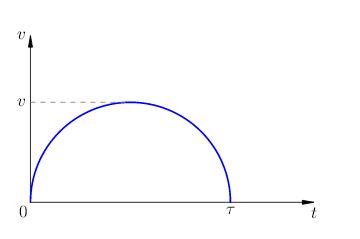
Sarcină. Viteza corp grafic este diametrul semicercul (Fig. 6). Viteza maximă a corpului este egală. Găsiți calea parcursă de-a lungul timpului organismul.

Decizie. După cum știți, aria unui cerc cu raza egală. Dar această problemă ar trebui să ia în considerare faptul că razele semicercuri au diferite dimensiuni: raza orizontală este timpul. iar gama verticală este viteza.

Prin urmare, distanța parcursă, care se calculează ca aria semicercului este egal cu jumătate din produsul pe raza orizontală și raza verticală: