Calcularea triplă integral 1

Curs 9.Vychislenie triplu integrală. sistem de coordonate curbilinii. Jacobi și semnificația sa geometrică. Schimbarea de variabile în mai multe integralelor. Tranziția la cilindrice și sferice coordonate triple integral.

Procedura este similară cu operarea de calcul integrală triplă corespunzătoare dublului integrală. Pentru a-l descrie, introducem conceptul unui domeniu tridimensional propriu-zis:

Definiția 9.1. Din regiunea tridimensională V, delimitat de suprafața S închisă, se numește regulat dacă:

1. Orice linie paralelă cu axa Oz și trasată prin zona punctului interior S intersectează în două puncte;
2. zona întregul V este proiectat pe xy-plan în mod regulat regiune D bidimensională;
3. Orice parte a regiunii V, separat de planul paralel sa la oricare dintre coordonate plane, are proprietățile 1) și 2).

Să considerăm o regiune V regulată, delimitată de suprafețele de sus și de jos z = χ (x, y) și z = ψ (x, y) și este proiectat pe planul xy în zona din dreapta D, în care x variază de la până la b, delimitate de curbele y = φ1 (x) și y = φ2 (x) (Fig.1). Definim în V funcție continuă f (x, y, z).

Definiție 9.2. Noi spunem că o triplă integrală a funcției f (x, y, z) regiunea V de expresie a formei:

De trei ori integrală are aceleași proprietăți ca și cea a dublului. Noi le enumăr fără dovezi, așa cum au dovedit într-un caz similar unui dublu integrală.

1. În cazul în care regiunea V împărțit în două zone V1 și V2 plan paralel cu oricare dintre coordonate plane, trei oară integral pe teren V este suma integralelor triplicat domeniilor V1 și V2.
2. Dacă m și M -, respectiv, cele mai mici și cele mai mari valori ale funcției f (x, y, z) în zona V, inegalitatea. mV ≤ IV ≤ MV, unde V - volumul actual al tehnicii, și IV - triplă integrală a funcției f (x, y, z) de V. câmp
3. IV integrală triplă a unei funcții f continuă (x, y, z) asupra regiunii V este produsul dintre volumul V asupra valorii funcției la o anumită regiune P punctul V: (9.2)

Calculul triplu integrale.

Teorema 9.1. integrală triplă a funcției f (x, y, z) pe zona din dreapta V este egală cu de trei ori integrala pe aceeași zonă:

Se împarte domeniul V plane paralele cu coordonate plane pentru regiunile corecte n. Apoi rezultă din 1 că

,

în care: - integralei triplă a funcției f (x, y, z) a câmpului.

Folosind formula (9.2), ecuația anterioară poate fi rescrisă ca:

.

Din funcția stării de continuitate f (x, y, z) rezultă că limita integralei sumei pe partea dreaptă a acestei ecuații, și există o triplă integrală. Apoi, trecând la limită, obținem:

QED.

În mod similar în cazul dublei integralei se poate demonstra că schimbarea în ordinea de integrare nu se schimba valoarea integralei triplu.

Exemplu. Se calculează integral unde V - o piramidă triunghiulară cu vârfuri la punctele (0, 0, 0), (1, 0, 0), (0, 1, 0) și (0, 0, 1). proiecția sa pe planul xy este triunghiul cu noduri (0, 0), (1, 0) și (0, 1). Regiunea inferioară este delimitată de planul z = 0, și de sus - planul x + y + z = 1. Ne întoarcem acum la o integrală triplă:

Factorii care nu depind de variabila de integrare, Bani, poate fi luat ca un semn al integralei corespunzătoare:

Sistemul de coordonate curbilinii în spațiul tridimensional.

1. Sistemul de coordonate cilindrice.

coordonatele cilindrice ale punctului P (ρ, φ, z) - este coordonatele polare ρ, proiecția φ a acestui punct pe planul Oxy și applicate un punct dat z (Fig.2).

Formulele pentru trecerea de la cilindrice la coordonate carteziene pot fi setate după cum urmează:

x = ρ cosφ, y = ρ sinφ, z = z. (9.4)

1. Sistemul de coordonate sferice.

În sferice coordonatele poziției punctului în spațiul determinat de liniar coordonate ρ - distanța de la un punct la începutul unui sistem de coordonate carteziene (sau poli de sistem sferice), φ - unghiul polar între pozitiv jumătate axa Ox și un punct de proiecție pe planul xy și θ - unghiul dintre axa semiaxis pozitivă oz și OP segment (Fig.3). În acest caz,

Definim formule pentru tranziția de la sferică la coordonate carteziene:

x = ρ sinθ cosφ, y = ρ sinθ sinφ, z = ρ cosθ. (9.5)

Jacobi și semnificația sa geometrică.

Luați în considerare cazul general de înlocuire a variabilelor într-un dublu integrală. Lăsați în domeniul dat D planul Oxy, delimitată de o linie L. Presupunem că x și y sunt funcții simple și în mod continuu diferențiabile noilor variabile u și v:

x = φ (u, v), y = ψ (u, v). (9.6)

Luați în considerare un sistem de coordonate OUV dreptunghiular, punctul P (u, v) care corespunde punctului P (x, y) ale regiunii D. Toate aceste puncte formează în planul regiunii D OUV delimitate de linia L. Se poate spune că formula (9.6) stabilește o corespondență unu la unu între punctele de zonele D și D. În acest caz, liniile u = const și

v = const în planul OUV va corespunde unora dintre liniile din planul Oxy.

Să considerăm un plan OUV δS suprafață dreptunghiulară, delimitată de liniile u = const, u + = const DU, v = const și v + = const Av. Ea se va întâlni cu δS platforma curbate în planul Oxy (Figura 4). Site-uri pătrate luate în considerare vor fi notate de asemenea și dS dS. Astfel δS = AU Av. Găsiți zona dS. Notăm vârfurile curbilinie patrulater P1, P2, P3, P4, în cazul în care

P1 (x1, y1), x1 = φ (u, v), y1 = ψ (u, v);

P2 (x2, y2), x2 = φ (u + AU, v), y2 = ψ (u + AU, v);

P3 (x3, y3), x3 = φ (u + AU, v + Av), Y3 = ψ (u + AU, v + Av);

P4 (x4, y4), x4 = φ (u, v + Av), y4 = ψ (u, v + Av).

Înlocuiți creșteri mici și AU diferențialele respective Av. atunci

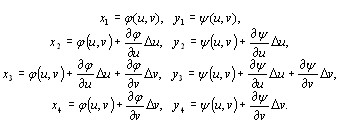
In acest patrulater P1 P2 P3 P4 poate presupune un paralelogram și determinarea zonei sale de formula din geometria analitică:

Definiția 9.3. Factorul determinant este numit determinant funcțional sau funcția Jacobian cp (x, y) și ψ (x, y).

Trecând la limită în (9.7), obținem sensul geometric al Jacobian:

modulul respectiv Jacobi este o limită a raportului suprafață de zone și dS dS infinitezimale.

Notă. În mod similar, putem defini conceptul de Jacobian și semnificația sa geometrică pentru spațiul n-dimensional: dacă x1 = φ1 (u1, u2, ..., ONU), x2 = φ2 (u1, u2, ..., ONU), ..., xn = φ (u1 , u2, ..., ONU),

În acest modul oferă limita Jacobian a raportului „volumul“ regiunilor mici de spațiu x1, x2, ..., xn și u1, u2, ..., ONU.

Schimbarea de variabile în mai multe integralelor.

Investigăm cazul general al unei schimbări de variabile pe exemplul unui dublu integrală.

In regiunea D este funcție continuă z = f (x, y), fiecare valoare care corespunde aceeași valoare a funcției z = F (u, v) în regiunea D, unde

F (u, v) = f (φ (u, v), ψ (u, v)). (9.9)

Luați în considerare suma integrală

în care suma integrală este preluată de zona din dreapta D. Închirierea obținem formula coordonatei de conversie într-o dublă integrală:

De asemenea, o formulă similară poate fi derivată pentru triplu integralei:

unde x = φ (u, v, w), y = ψ (u, v, w), z = χ (u, v, w),

și regiunea spațiul V Oxyz este afișat în spațiul V Ouvw.

Tranziția către cilindrice și sferice coordonate

în triplu integrală.

Constatăm, folosind formula (9.4), (9,5) și (9.12), Jacobians tranziție de la coordonate carteziene la cilindrice și sferice:

1. coordonate cilindrice

1. pentru coordonate sferice

Apoi, în formulele integrale triple pentru trecerea la cilindrice sau sferice coordonatele vor fi: (9.15)

,

în cazul în care sensul notația este clar din textul precedent.

1. Calculăm integralei unei funcții a zonei delimitate de suprafețe x² + 1 = Ya, y = 0, y = x, z = 0, z = 1.

1. Fie u integrandul = 1, și regiunea de integrare - o minge de rază R centrată la origine. atunci

.

Mama tuturor instrument de luare a fost specialități departamentul de „Mecanică Fină Dispozitive“, care a fost deschis în 1961 la Facultatea de Inginerie Mecanică.
În 1976, a fost organizat departamentul opto-mecanic.