Algebra în clasa a opta, soluție grafică clasa de ecuații pătratice
Prezentarea și lecția pe „soluție grafică a ecuațiilor pătratice“
manuale de formare și simulatoare de magazin on-line „Integral“ pentru clasa a 8-a
Gradul și rădăcini Funcții și grafice
Grafice de funcții pătratice
În ultima lecție am învățat cum să construiască un grafic al oricărei funcții pătratice. Cu ajutorul acestor funcții, putem rezolva așa-numitele ecuațiile pătratice, care sunt scrise în formă generală, după cum urmează: $ ax ^ 2 + bx + c = 0 $,
$ A, b, c $ - orice număr, dar $ a ≠ 0 $.
Baieti, compara ecuația scrisă mai sus și acest lucru: $ y = ax ^ 2 + bx + c $.
Ele sunt aproape identice. Diferența este că, în loc de $ y $ am înregistrat $ 0 $, adică, $ Y = 0 $. Cum apoi pentru a rezolva ecuații pătratice? Primul lucru care vine în minte, este necesar să se complot $ parabolei ax ^ 2 + bx + c $ și pentru a găsi punctul de intersecție al graficului cu linia $ y = 0 $. Există și alte modalități de a rezolva. Luați în considerare exemplul concret.
Metode de rezolvare a funcțiilor pătratice
Exemplu.
Rezolva ecuația: $ x ^ 2 + 2x-8 = 0 $.
Decizie.
1. O metodă construi graficul de $ y = x ^ 2 + 2x-8 $ și găsi punctul de intersecție cu linia $ y = 0 $. Coeficientul de cea mai mare putere este pozitiv, atunci ramura parabolei uita în sus. Noi găsim coordonatele nodurilor:
$ X _ = - \ frac = \ frac = -1 $.
$ Y _ = (- 1) ^ 2 + 2 * (- 1) -8 = 1-2-8 = $ -9.
Punct cu coordonatele $ (- 1; -9) $ este luată ca începutul unui nou sistem de coordonate și de a construi în său program parabole $ y = x ^ 2 $.
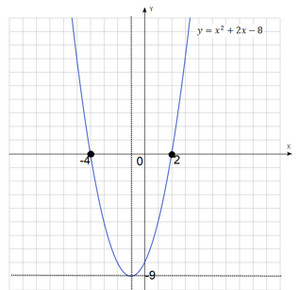
Vedem două puncte de intersecție. Acestea sunt marcate cu puncte negre de pe grafic. Noi rezolva ecuația pentru x, deci ar trebui să selectați abscisă acestor puncte. Acestea sunt $ -4 $ și $ 2 $.
Astfel, soluția ecuației pătratice $ x ^ 2 + 2x-8 = 0 $ două rădăcini: $ x_1 = -4 $ și $ x_2 = $ sau 2.
Metoda 2: Transformarea ecuația originală la forma: $ x ^ 2 = 8-2x $.
In acest fel putem rezolva această ecuație prin metoda grafică obișnuită, găsirea absciselor punctelor de intersecție a două grafice $ y = x ^ 2 $ și $ y = 8-2x $.
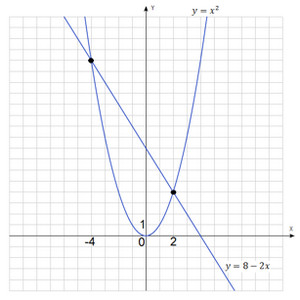
Câștigat două puncte de intersecție, dintre care abscisa coincid cu cele obținute în primele soluții de proces, și anume: $ x_1 = -4 $ și $ x_2 = 2 $.
Metoda 3.
Noi transformăm ecuația originală pentru această formă: $ x ^ 2-8 = -2x $.
Noi construim două grafice de $ y = x ^ 2-8 $ și $ y = -2x $ și pentru a găsi punctul lor de intersecție.
Program $ y = x ^ 2-8 $ parabolei este compensată de 8 unități în jos.
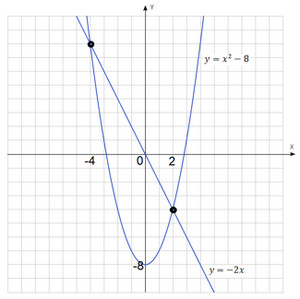
A primit două puncte de intersecție, abscisa acestor puncte sunt aceleași ca și în cele două metode anterioare, și anume: $ x_1 = -4 $ și $ x_2 = $ sau 2.
Metoda 4.
Isolate un pătrat complet în ecuația originală: $ x ^ 2 + 2x-8 = x ^ 2 + 2x + 1-9 = (x + 1) ^ $ 2-9.
Am construit două grafice ale funcțiilor $ y = (x + 1) ^ 2 $ și $ y = $ 9. Graficul primei funcție este un parabole deplasat cu o unitate la stânga. Graficul a doua funcție - este o linie paralelă cu axa x și care trece prin ordonata egală cu $ 9 $.
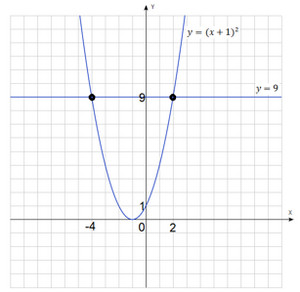
Încă o dată, a primit două puncte de intersecție a graficelor, abscisă acestor puncte coincid cu cele obținute în procesele anterioare $ x_1 = -4 $ și $ x_2 = 2 $.
Metoda 5.
Vom împărți ecuația originală de x: $ \ frac + \ fracturate \ Frac = \ frac $.
$ X + 2- \ frac = 0 $.
$ X + 2 = \ frac $.
Vom rezolva această ecuație construi grafic două grafice $ y = x + 2 $ și $ y = \ frac $.
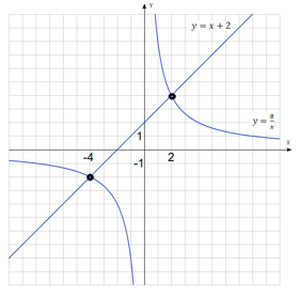
a primit din nou două puncte de intersecție, abscisa punctelor coincid cu cele obținute mai sus $ x_1 = -4 $ și = $ 2 $ x_2.
Soluție grafică Algoritmul de funcții pătratice
Băieți, am considerat cinci metode de soluții grafice de ecuații pătratice. In fiecare dintre aceste moduri rădăcini de ecuații s-au dovedit la fel, ceea ce înseamnă că se obține soluția corectă.
Principalele metode de soluții grafice de ecuații pătratice $ ax ^ 2 + bx + c = 0 $, $ a, b, c $ - orice număr, dar $ a ≠ 0 $:
1. Construirea unui grafic de $ y = ax ^ 2 + bx + c $, găsi un punct de intersecție cu axa x, care va fi soluția ecuației.
2. construi două grafice $ y = ax ^ 2 $ și $ y = -bx-C $, găsiți abscisa punctelor de intersecție ale acestor grafice.
3. construi două grafice $ y = ax ^ 2 + c $ și $ y = $ -bx, găsiți abscisa punctelor de intersecție ale acestor grafice. Graficul primei funcției este o parabolă, sau mutat în jos sau în sus, în funcție de numărul de semn s. In al doilea grafic - linia care trece prin origine.
4. Selectați un pătrat perfect, care este, aduce ecuația originală la forma: $ a (x + l) ^ 2 + m = 0 $.
Pentru a construi două din graficul de $ y = a (x + l) ^ 2 $ și $ y = -m $, găsi punctul lor de intersecție. Graficul din prima funcție este un parabole mutat fie la stânga sau la dreapta, în funcție de semnul numărului $ l $. Graficul a doua funcție este o linie dreaptă paralelă cu axa absciselor și axa ordonată care se intersectează într-un punct egal cu $ -m $.
5. Se împarte ecuația originală de x: $ ax + b + \ frac = 0 $.
Conversia la forma: $ \ Frac = -ax-b $.
construi din nou două grafice și pentru a găsi puncte de intersecție. Primul grafic - hiperbola, al doilea grafic - este drept. Din păcate, metoda grafică pentru rezolvarea ecuațiilor de gradul doi nu este intotdeauna o modalitate buna de a rezolva. Punctele de intersecție ale diferitelor diagrame nu sunt întotdeauna numere întregi sau pot avea în abscisă (ordonata) un număr foarte mare, care nu se bazează pe o foaie de hârtie standard.
demonstrează mai clar toate aceste tehnici prin exemple.
Exemplu.
Rezolva ecuația: $ x ^ 2 + 3x-12 = 0 $,
Decizie.
Noi construim graficul parabolei și pentru a găsi coordonatele nodurilor: $ x _ = - \ frac = \ frac = -1,5 $.
$ Y _ = (- 1,5) ^ 2 + 2 * (- 1,5) -8 = 2,25-3-8 = -8,75 $.
La construirea unei parabole atunci când apar probleme, de exemplu, pentru a marca în mod corespunzător în partea de sus a parabolei. Pentru a marca cu exactitate nodurile ordonatelor nevoie pentru a selecta o celulă, egală cu 0,25 unități de scală. La această scară pentru a merge în jos de 35 de unități în jos, care este incomod. Tot la fel, vom construi programul nostru.
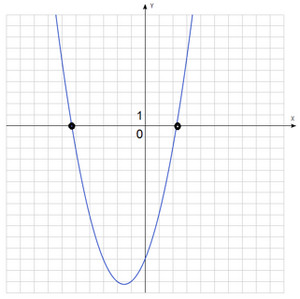
A doua problemă cu care ne confruntăm este că graficul nostru funcție traversează axa x la punctul cu coordonatele care indică cu precizie imposibil. Poate o soluție aproximativă. dar matematica - este o știință exactă.
Astfel, metoda grafică nu este cel mai convenabil. Prin urmare, pentru a rezolva ecuații pătratice necesită o metodă universală, pe care o vom explora în lecția următoare.
Sarcini pentru decizia independentă
1. Rezolva ecuatia grafic (toate cele cinci moduri): $ x ^ 2 +-4x 12 = 0 $.
2. Rezolva ecuație orice formă grafică: -x $ ^ 2 + 6x $ + 16 $ = 0.